
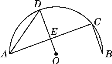
【题目】如图,AB是半圆O的直径,C,D是半圆O上的两点,OD∥BC,OD与AC交于点E.
(1)若∠D=70°,求∠CAD的度数;
(2)若AC=8,DE=2,求AB的长.
【答案】(1) 20°;(2) 10.
【解析】
(1)根据圆周角定理可得∠ACB=90°,则∠CAB的度数即可求得,在等腰△AOD中,根据等边对等角求得∠DAO的度数,则∠CAD即可求得;
(2)设OA=x,则OE=OD-DE=x-2. 在Rt△OAE中利用勾股定理即可求解.
解:(1)∵OA=OD,∠D=70°,
∴∠OAD=∠D=70°.
∴∠AOD=180°-∠OAD-∠D=40°.
∵AB是半圆O的直径,
∴∠C=90°.
∵OD∥BC,
∴∠AEO=∠C=90°,即OD⊥AC.
∴![]() =
=![]() .
.
∴∠CAD=![]() ∠AOD=20°.
∠AOD=20°.
(2)由(1)可知OD⊥AC,
∴AE=![]() AC=
AC=![]() ×8=4.
×8=4.
设OA=x,则OE=OD-DE=x-2.
在Rt△OAE中,OE2+AE2=OA2,
即(x-2)2+42=x2,解得x=5.
∴AB=2OA=10.


科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.小东根据学习函数的经验,对函数
的图象与性质.小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是x与y的几组对应值.
| ... |
|
|
|
|
|
|
| 1 | 2 | 3 | ... |
| ... |
|
|
|
|
|
|
|
|
| m | ... |
求m的值;
(3)如图,在平面直角坐标系中,已描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,![]() ).结合函数的图象,写出该函数的其它性质(写两条即可).
).结合函数的图象,写出该函数的其它性质(写两条即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是25cm,AC的长为5cm,求线段AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化工材料经销公司购进一种化工原料若干千克,价格为每千克30元。物价部门规定其销售单价不高于每千克60元,不低于每千克30元。经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100。在销售过程中,每天还要支付其他费用450元。
(1)求出y与x的函数关系式,并写出自变量x的取值范围。
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式。
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O与等腰直角三角形两腰CA,CB分别切于D,E两点,直径FG在AB上,若BG=![]() -1,则△ABC的周长为( )
-1,则△ABC的周长为( )

A. 4+2![]() B. 6 C. 2+2
B. 6 C. 2+2![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过m(30<m≤100)人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队,收取总费用为y元.
(1)求y关于x的函数表达式;
(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均毎天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调査表明:这种冰箱的售价毎降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价![]() 元,商场每天销售这种冰箱的利润为
元,商场每天销售这种冰箱的利润为![]() 元,请写出
元,请写出![]() 与
与![]() 间的函数表达式;(不要求写出自变量的取值范围)
间的函数表达式;(不要求写出自变量的取值范围)
(2)商场要想在这种冰箱销售中毎天盈利4800元,同时又要使百姓得到实惠,毎台冰箱应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC= °.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bc+c的图象如图所示,则下列判断中错误的是( )

A. 图象的对称轴是直线x=﹣1 B. 当x>﹣1时,y随x的增大而减小
C. 当﹣3<x<1时,y<0 D. 一元二次方程ax2+bx+c=0的两个根是﹣3,1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com