
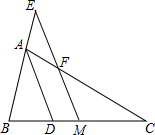
 如图,在△ABC中,AD是∠BAC的平分线,M是BC的中点,过M作ME∥AD交BA延长线于E,交AC于F,求证:BE=CF=$\frac{1}{2}$(AB+AC).
如图,在△ABC中,AD是∠BAC的平分线,M是BC的中点,过M作ME∥AD交BA延长线于E,交AC于F,求证:BE=CF=$\frac{1}{2}$(AB+AC). 分析 首先过点B作BN∥AC交EM的延长线于点N,然后判断出BN=CF,BN=BE,即可判断出BE=CF;最后根据∠EFA=∠CFM,可得∠E=∠EFA,AE=AF,所以AB+AC=AB+(AF+CF)=AB+AE+CF=BE+CF,据此判断出BE=CF=$\frac{1}{2}$(AB+AC)即可.
解答 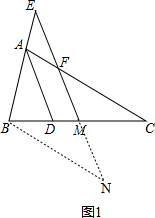 证明:如图1,过点B作BN∥AC交EM的延长线于点N,
证明:如图1,过点B作BN∥AC交EM的延长线于点N,
∵M是BC的中点,
∴BM=CM,
∵BN∥AC,
∴$\frac{BN}{CF}=\frac{BM}{CM}$=1,∠CFM=∠N,
∴BN=CF;
∵ME∥AD,
∴∠E=∠BAD,∠CFM=∠CAD,
又∵AD是∠BAC的平分线,
∴∠BAD=∠CAD,
∴∠E=∠CFM,
又∵∠CFM=∠N,
∴∠E=∠N,
∴BN=BE,
∴BE=CF;
∵∠EFA=∠CFM,
∴∠E=∠EFA,
∴AE=AF,
∴AB+AC=AB+(AF+CF)=AB+AE+CF=BE+CF,
∴BE=CF=$\frac{1}{2}$(AB+AC).
点评 此题主要考查了三角形中位线定理的应用,要熟练掌握,解答此题的关键是要明确:三角形的中位线平行于第三边,并且等于第三边的一半.


科目:初中数学 来源: 题型:选择题
| A. | 自左平移3个单位长度得到的 | B. | 向右平移3个单位长度得到的 | ||
| C. | 向上平移3个单位长度得到的 | D. | 向下平移3个单位长度得到的 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在四边形ABCD中,∠BCD=∠BAD=90°,AC,BD相交于点E,点G,H分别是AC,BD的中点,若∠BEC=80°,那么∠GHE等于( )
如图,在四边形ABCD中,∠BCD=∠BAD=90°,AC,BD相交于点E,点G,H分别是AC,BD的中点,若∠BEC=80°,那么∠GHE等于( )| A. | 5° | B. | 10° | C. | 20° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “低碳生活,绿色出行”的理念正逐渐被人们所接受,越来越多的人选择骑自行车上下班,王叔叔某天骑自行车上班,从家出发到单位过程中行进速度v(米/分钟)随时间t(分钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l过点T且与横轴垂直,梯形OABC在直线l左侧部分的面积即为t分钟内王叔叔行进的路程s(米).
“低碳生活,绿色出行”的理念正逐渐被人们所接受,越来越多的人选择骑自行车上下班,王叔叔某天骑自行车上班,从家出发到单位过程中行进速度v(米/分钟)随时间t(分钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l过点T且与横轴垂直,梯形OABC在直线l左侧部分的面积即为t分钟内王叔叔行进的路程s(米).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1)(1,2),(2,2),…,根据这个规律,第2015个点的坐标为(45,10).
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1)(1,2),(2,2),…,根据这个规律,第2015个点的坐标为(45,10).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
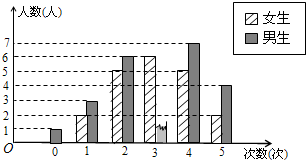 为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看3次的人数没有标出).
为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看3次的人数没有标出).| 统计量 | 平均数(次) | 中位数(次) | 众数(次) | 方差 | … |
| 该班级男生 | 3 | 3 | 4 | 2 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
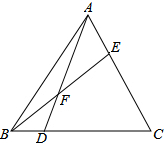 如图,已知点D、E分别是△ABC边BC、AC上的点,AD与BC相交于点F,且$\frac{BD}{DC}$=$\frac{1}{3}$,$\frac{AE}{AC}$=$\frac{1}{5}$,求$\frac{AF}{AD}$的值.
如图,已知点D、E分别是△ABC边BC、AC上的点,AD与BC相交于点F,且$\frac{BD}{DC}$=$\frac{1}{3}$,$\frac{AE}{AC}$=$\frac{1}{5}$,求$\frac{AF}{AD}$的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com