练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．先化简，再求值：（a-$\sqrt{2}$）（a+$\sqrt{2}$）+a（3-a），其中a=-2．

    分析 原式利用平方差公式，以及单项式乘多项式法则计算，合并得到最简结果，把a的值代入计算即可求出值．

    解答 解：原式=a2-2+3a-a2=3a-2，
    当a=-2时，原式=3×（-2）-2=-8．

    点评 此题考查了整式的混合运算-化简求值，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    6．如图，在?ABCD中，AD⊥BD，点E、F分别在AB、BD上且满足AD=AE=DF，连接DE、AF、EF．
    （1）若∠CDB=30°，求∠EAF的度数；
    （2）若DE⊥EF，求证：DE=2EF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．某电压力锅生产厂家计划每天平均生产n台电压力锅，而实际产量与计划产量相比有出入．下表记录了某周五个工作日每天实际产量情况（超过计划产量记为正、少于计划产量记为负）：
    星期一二三四五
    实际生产量/台+7-2-3+11-4
    （1）用含n的代数式表示本周前三天生产电压力锅的总台数；
    （2）该厂实行每日计件工资制：每生产一台电压力锅可得60元，若超额完成任务，则超过部分每台另奖15元；少生产一台扣20元．当n=100时，那么该厂工人这一周的工资总额是多少元？
    （3）若将上面第（2）问中“实行每日计件工资制”改为“实行每周计件工资制”，其他条件不变，当n=100时，在此方式下这一周工人的工资与按日计件的工资哪一个更多？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，正方形ABCD的对角线相交于点O，点E，F分别在OA，OB上，且OE=OF，BE和CF有特殊的大小关系吗？BE和CF有特殊的位置关系吗？证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．某校对学生上学方式进行了一次抽样调查，如图是根据此次调查结果所绘制的一个未完成的扇形统计图，已知该校学生共有2000人，被调查的学生中乘车的有9人，则下列四种说法中，错误的是（　　）
    A．被调查的学生有60人
    B．被调查的学生中，步行的有27人
    C．估计全校骑车上学的学生有700人
    D．扇形图中，乘车部分所对应的圆心角为15°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．某城市居民用水实行阶梯收费，每户每月用水量如果未超过20吨，按每吨1.9元收费．如果超过20吨，未超过的部分按每吨1.9元收费，超过的部分按每吨2.8元收费．设某户每月用水量为x吨，应收水费为y元．
    （1）设某户居民每月用水量为m吨（m≤20），则应收水费为y=1.9x元（用含m的代数式表示）；
    （1）设某户居民每月用水量为m吨（m＞20），则应收水费为2.8x-18元（用含m的代数式表示）；
    （2）若该城市某户5月份水费平均为每吨2.2元，求该户5月份用水多少吨？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．一个三位数，百位上的数是c，十位上的数是b，个位上的数是a，则该三位数是（　　）
    A．abcB．a+10b+100cC．100a+10b+cD．a+b+c

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．先化简，再求值．$3{x^2}y-[2xy-2（xy-\frac{3}{2}{x^2}y）]+{x^2}{y^2}$，其中x=3，y=$-\frac{1}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

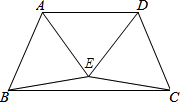    6．如图，△ABE与△CDE是两个全等的等边三角形，且EA⊥ED．有下列四个结论：（1）∠EBC=15°；（2）AD∥BC；（3）直线CE与AB垂直；（4）四边形ABCD是轴对称图形．其中正确的结论有（　　）
    A．4个B．3个C．2个D．1个

    查看答案和解析>>

    同步练习册答案