
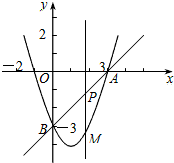
 ��ͼ����ƽ��ֱ������ϵ�У�������y=x2-2x-3��ֱ��y=x-3������A��B����P��ֱ��AB�ϵĶ��㣬����P��x��Ĵ��߽��������ڵ�M�����P�ĺ�����Ϊt��
��ͼ����ƽ��ֱ������ϵ�У�������y=x2-2x-3��ֱ��y=x-3������A��B����P��ֱ��AB�ϵĶ��㣬����P��x��Ĵ��߽��������ڵ�M�����P�ĺ�����Ϊt������ ��1��һ�ַ��������������������꣬��һ�ַ����ǽ��������������ʽ���ɣ�
��2���ú�t��ʽ�ӱ�ʾ����P����M �����꣬�ú�t��ʽ�ӱ�ʾ��PM�ij��������PM���ʱt��ֵ�����ݷָ�����ABM��������ɣ�
��3�����ݵ�P�IJ�ͬλ�ã�������������ۣ���0��t��3ʱ����t��3ʱ����t��0ʱ���ú�t��ʽ�ӱ�ʾ�߶�PM��ֵ������ƽ���ı��ε��ж�������һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ���PM=OB�����t��ֵ���ɣ�
��� �⣺��1������һ������������$\left\{\begin{array}{l}{y={x}^{2}-2x-3}\\{y=x-3}\end{array}\right.$�������ꣻ
������������A��3��0������B��0��-3���ֱ���������ߺ�ֱ�ߵĽ���ʽ���жϵ�A����B�Ƿ��������ߺ�ֱ���ϣ�
��2���ɵ�P��ֱ��ABy=x-3�ϣ��ɵã���x=tʱ��y=t-3������P��t��t-3����
�ɵ�M��������y=x2-2x-3�ϣ��ɵã���x=tʱ��y=t2-2t-3������M��t��t2-2t-3����
����P���߶�AB��ʱ��PM=t-3-��t2-2t-3��=t-3-t2+2t+3=-t2+3t=$-��t-\frac{3}{2}��^{2}+\frac{9}{4}$��
�൱t=$\frac{3}{2}$ʱ��PM������ֵΪ$\frac{9}{4}$��
S��ABM=S��APM+S��BPM=$\frac{1}{2}��\frac{9}{4}��\frac{3}{2}+\frac{1}{2}��\frac{9}{4}��\frac{3}{2}=\frac{27}{8}$��
��3�����ڣ�
���ɣ���0��t��3ʱ����ͼ1��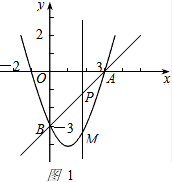
�����⣬��֪��OB��PM��Ҫʹ�ı���OBPM��ƽ���ı��Σ�������OB=PM���ɣ�
�ɣ�2����֪��PM�����ֵΪ$\frac{9}{4}$��
����PM����OB��
����������ĵ�P��ʹ���ı���OBPM��ƽ���ı��Σ�
��t��3ʱ����ͼ2��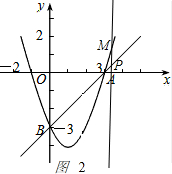
��ʱ��PM=t2-2t-3-t+3=t2-3t��
�����⣬��֪��OB��PM��Ҫʹ�ı���OBPM��ƽ���ı��Σ�������OB=PM���ɣ�
��t2-3t=3����ã�${t}_{1}=\frac{3+\sqrt{21}}{2}$��${t}_{2}=\frac{3-\sqrt{21}}{2}$���������⣬��ȥ����
��t��0ʱ����ͼ3��
��ʱ��PM=t2-2t-3-t+3=t2-3t��
�����⣬��֪��OB��PM��Ҫʹ�ı���OBPM��ƽ���ı��Σ�������OB=PM���ɣ�
��t2-3t=3����ã�${t}_{1}=\frac{3+\sqrt{21}}{2}$���������⣬��ȥ����${t}_{2}=\frac{3-\sqrt{21}}{2}$��
������������P�������$\frac{3+\sqrt{21}}{2}$��${t}_{2}=\frac{3-\sqrt{21}}{2}$��
���� ������Ҫ������κ������ۺ�Ӧ�ã�������ѵ㲻�ڣ�2��С�⣬���������÷ָ�������ε�����ǽ���Ĺؼ����ڣ�3��С�⣬�ܹ��뵽���ݵ�P�IJ�ͬλ�ý��з��������ǽ������ؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | -2 | C�� | 0 | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
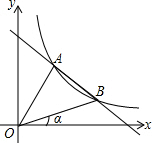 ��ͼ��ֱ��y=kx+b��k��0�����뷴��������y=$\frac{m}{x}$��m��0����ͼ���ڵ�һ�����ڵ�A��B���㣬��֪��A������Ϊ��3��4����OB��x��������ļн�Ϊ������tan��=$\frac{1}{3}$��
��ͼ��ֱ��y=kx+b��k��0�����뷴��������y=$\frac{m}{x}$��m��0����ͼ���ڵ�һ�����ڵ�A��B���㣬��֪��A������Ϊ��3��4����OB��x��������ļн�Ϊ������tan��=$\frac{1}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-3��3=-9 | B�� | $\sqrt{��-4��^{2}}$=-4 | C�� | -|-5|=5 | D�� | ��$\frac{1}{2}$��-3=8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
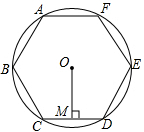 ��ͼ����֪��O���ܳ�����8��cm����Բ�ڽ���������ABCDEF�ı��ľ�OM�ij�Ϊ��������
��ͼ����֪��O���ܳ�����8��cm����Բ�ڽ���������ABCDEF�ı��ľ�OM�ij�Ϊ��������| A�� | 2cm | B�� | 2$\sqrt{3}$cm | C�� | 4cm | D�� | 4$\sqrt{3}$cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AC�Ǿ���ABCD�ĶԽ��ߣ�������ֽƬ�۵���ʹ��C���A�غϣ�����ͼ�л����ۺۣ�Ȼ������ͼ�л�������ABCD�����Բ�����ó߹���ͼ��д�����ۣ���д������������ͼ�ۼ���������ͼ�ۼ��ú�ɫǩ�ֱʼӺڣ���
��ͼ��AC�Ǿ���ABCD�ĶԽ��ߣ�������ֽƬ�۵���ʹ��C���A�غϣ�����ͼ�л����ۺۣ�Ȼ������ͼ�л�������ABCD�����Բ�����ó߹���ͼ��д�����ۣ���д������������ͼ�ۼ���������ͼ�ۼ��ú�ɫǩ�ֱʼӺڣ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
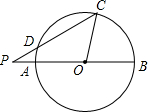 ��ͼ����֪AB�ǡ�O��ֱ����AB=16����P��AB����ֱ����һ�㣬OP=10����C�ǡ�O��һ�㣬PC����O�ڵ�D��sin��BPC=$\frac{3}{5}$����CD�ij���
��ͼ����֪AB�ǡ�O��ֱ����AB=16����P��AB����ֱ����һ�㣬OP=10����C�ǡ�O��һ�㣬PC����O�ڵ�D��sin��BPC=$\frac{3}{5}$����CD�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
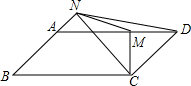 ��ͼ����?ABCD�У�AD=2AB��CM��AD��CN��AB������ֱ�ΪM��N������MN��ND�������н���һ����ȷ���Ǣ٢ڢۢܣ����뽫��������ں����ϣ�
��ͼ����?ABCD�У�AD=2AB��CM��AD��CN��AB������ֱ�ΪM��N������MN��ND�������н���һ����ȷ���Ǣ٢ڢۢܣ����뽫��������ں����ϣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com