
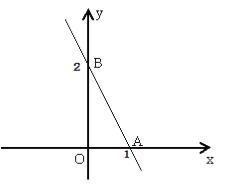
����Ŀ����һ����С��һ���Լ�ȥ���360km��ij�����棬ȫ�̵�ǰһ����Ϊ���ٹ�·����һ����Ϊ��幫·����С�����ڸ��ٹ�·����幫·�Ϸֱ���ijһ�ٶ�������ʻ����ʻ��·��y����λ��km����ʱ��x����λ��h��֮��Ĺ�ϵ��ͼ��ʾ�������н�����ȷ���ǣ�������
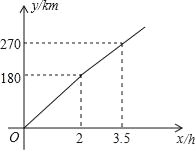
A. С��������幫·�ϵ���ʻ�ٶ�Ϊ60km/h
B. С�����ڸ��ٹ�·�ϵ���ʻ�ٶ�Ϊ120km/h
C. ��幫·�ܳ�Ϊ90km
D. С�����ڳ�����5.5h����Ŀ�ĵ�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
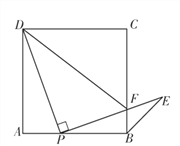
����Ŀ����ͼ����P��������ABCD��AB��һ�㣨��P�����A��B�غϣ�������PD�����߶�PD�Ƶ�P˳ʱ�뷽����ת90��õ��߶�PE��PE����BC�ڵ�F������BE��DF.
��1�����PBE�Ķ�����
��2������PFD�ס�BFP����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
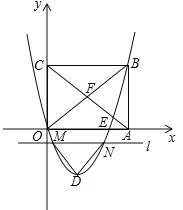
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�ı�OA��OC�ֱ���x�ᡢy���ϣ���B����Ϊ��4��t����t��0�������κ���![]() ��b��0����ͼ����B������Ϊ��D��
��b��0����ͼ����B������Ϊ��D��
��1����t=12ʱ������D��x��ľ������ ��
��2����E�Ƕ��κ���![]() ��b��0����ͼ����x���һ�������㣨��E���O���غϣ�����OEEA�����ֵ��ȡ�����ֵʱ�Ķ��κ�������ʽ��
��b��0����ͼ����x���һ�������㣨��E���O���غϣ�����OEEA�����ֵ��ȡ�����ֵʱ�Ķ��κ�������ʽ��
��3������OABC�ĶԽ���OB��AC���ڵ�F��ֱ��lƽ����x�ᣬ�����κ���![]() ��b��0����ͼ���ڵ�M��N������DM��DN������DMN�ա�FOCʱ����t��ֵ��
��b��0����ͼ���ڵ�M��N������DM��DN������DMN�ա�FOCʱ����t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
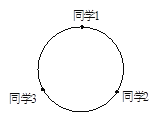
����Ŀ���Ķ����⣺һ����ͬѧΧ��һ��������������Ϸ, ���ǰ�ijͬѧ���������ͬѧ������Ϊ��ͬѧ����������. ��Ϸ������: ͬѧ1���������һ����, �����������2�ټ�1��ͬѧ2��ͬѧ2��ͬѧ1��������������2�ټ�![]() ��ͬѧ3��ͬѧ3��ͬѧ2��������������2�ټ�1��ͬѧ4��ͬѧ4��ͬѧ3��������������2�ټ�
��ͬѧ3��ͬѧ3��ͬѧ2��������������2�ټ�1��ͬѧ4��ͬѧ4��ͬѧ3��������������2�ټ�![]() ��ͬѧ5��ͬѧ5��ͬѧ4��������������2�ټ�1��ͬѧ6�������������������ɣ��������ǰ���ͬѧ�������δ����������ͬѧ��ֱ��������ͬѧ1Ϊֹ.
��ͬѧ5��ͬѧ5��ͬѧ4��������������2�ټ�1��ͬѧ6�������������������ɣ��������ǰ���ͬѧ�������δ����������ͬѧ��ֱ��������ͬѧ1Ϊֹ.
��1����ֻ��ͬѧ1��ͬѧ2��ͬѧ3������������Ϸ.
��ͬѧ1������õ�����2, ��ͬѧ3������������ ��
��������ͬѧ����������֮��Ϊ17����ͬѧ1��������õ����� .
��2������![]() ��ͬѧ��nΪ����1��ż����������������Ϸ����
��ͬѧ��nΪ����1��ż����������������Ϸ����![]() ��ͬѧ����������֮��Ϊ
��ͬѧ����������֮��Ϊ ![]() ����ͬѧ1��������õ����Ƕ���.
����ͬѧ1��������õ����Ƕ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
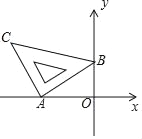
����Ŀ����ͼ����ֱ������ϵ�У�ֱ����x���ཻ�ڵ�A����y���ཻ�ڵ�B.
��1��ֱ��д��A�������__________��
��2����x__________ʱ��y��4��
��3����B����ֱ��BP��x���ཻ��P����OP=2OAʱ������ABP�������
(4) ��y�����Ƿ����E�㣬ʹ����ABEΪ����������,�����ڣ�ֱ��д������������E������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����CΪ��ABD���Բ�ϵ�һ���㣨��C����![]() �����Ҳ����B��D�غϣ�����ACB=��ABD=45����
�����Ҳ����B��D�غϣ�����ACB=��ABD=45����
��1����֤��BD�Ǹ����Բ��ֱ����
��2������CD����֤�� ![]() AC=BC+CD��
AC=BC+CD��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����в��ϣ�
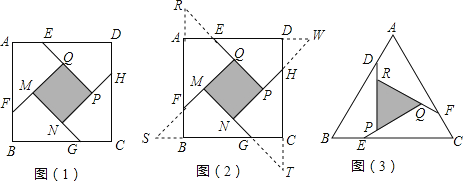
С����������һ�����⣺��ͼ1���ڱ߳�Ϊa(a��2)��������ABCD�����Ϸֱ��ȡAE=BF=CG=DH=1������AFQ=��BGM=��GHN=��DEP=45��ʱ����������MNPQ�������
С�����֣��ֱ��ӳ�QE��MF��NG��PH��FA��GB��HC��ED���ӳ����ڵ�R��S��T��W���ɵ���RQF����SMG����TNH����WPE���ĸ�ȫ�ȵĵ���ֱ��������(��ͼ2) ��
��ش�
(1)���������ĸ�����ֱ��������ƴ��һ���µ�������(��϶���ص�)��������������εı�Ϊ ��
(2)��������MNPQ�������
(3)�ο�С��˼������ķ�����������⣺
��ͼ3���ڵȱ���ABC�����Ϸֱ��ȡAD=BE=CF���ٷֱ����D��E��F��BC��AC��AB�Ĵ��ߣ��õ��ȱ���RPQ����S��RPQ=![]() ����AD�ij���
����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������45���ǵ�ֱ�����dz߷�����ƽ��ֱ������ϵ�У�����A����2��0����B��0��1������ֱ��BC�ĺ�������ʽΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
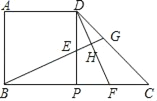
����Ŀ����֪��������ABPD�ı߳�Ϊ3������DP�Ƶ�P˳ʱ����ת90����PC��E��F�ֱ�Ϊ�߶�DP��CP���������㣨����D��P��C�غϣ�����DE=CF������BE���ӳ��ֱ�DF��DC��H��G��
��1������֤����BPE�ա�DPF�����ж�BG��DFλ�ù�ϵ��˵�����ɣ�
��2����PE�ij���Ϊ����ʱ���ı���DEFGΪ���β�˵�����ɣ�
��3������AH���ڵ�E��F�˶��Ĺ����У���AHB�Ĵ�С�Ƿ����ı䣿���ı䣬��˵������α仯�ģ������ı䣬�������AHB�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com