
����Ŀ��ij��˾��Ӫ��÷ҵ����3��Ԫ/�ֵļ۸���ũ���չ���÷�ּ��A��B���࣬A����÷��װ��ֱ�����ۣ�B����÷��ӹ��������ۣ�A����÷�İ�װ�ɱ�Ϊ1��Ԫ/�֣������г����飬����ƽ�����ۼ۸�y����λ����Ԫ/�֣�����������x��x��2��֮��ĺ�����ϵ��ͼ��B����÷��ӹ��ܷ���s����λ����Ԫ����ӹ�����t����λ���֣�֮��ĺ�����ϵ��s=12+3t��ƽ�����ۼ۸�Ϊ9��Ԫ/�֣� 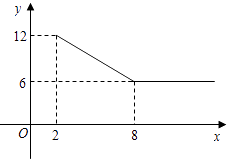
��1��ֱ��д��A����÷ƽ�����ۼ۸�y��������x֮��ĺ�����ϵʽ��
��2����һ�Σ��ù�˾�չ���20����÷������A����÷��x�֣���Ӫ������÷����õ�ë����Ϊw��Ԫ��ë����=���������멁��Ӫ�ܳɱ����� ����w����x�ĺ�����ϵʽ��
�����ù�˾�����30��Ԫë�����ʣ�����ֱ����A����÷�ж��ٶ֣�
��3���ڶ��Σ��ù�˾��Ͷ��132��Ԫ�ʽ������һ�־�Ӫ������ʹ��˾������ë����������ë����
���𰸡�
��1���⣺�ٵ�2��x��8ʱ����ͼ��

��ֱ��AB����ʽΪ��y=kx+b��
��A��2��12����B��8��6������ã�
![]() �����
����� ![]() ��
��
��y=��x+14��
�ڵ�x��8ʱ��y=6��
����A����÷ƽ�����ۼ۸�y��������x֮��ĺ�����ϵʽΪ��
y= ![]()
��2���⣺������A����÷x�֣�������B����÷��20��x���֣�
�ٵ�2��x��8ʱ��
wA=x����x+14����x=��x2+13x��
wB=9��20��x����[12+3��20��x��]=108��6x
��w=wA+wB��3��20
=����x2+13x��+��108��6x����60
=��x2+7x+48��
��x��8ʱ��
wA=6x��x=5x��
wB=9��20��x����[12+3��20��x��]=108��6x
��w=wA+wB��3��20
=��5x��+��108��6x����60
=��x+48��
��w����x�ĺ�����ϵʽΪ��
w= ![]() ��
��
�ڵ�2��x��8ʱ����x2+7x+48=30�����x1=9��x2=��2�����������⣻
��x��8ʱ����x+48=30�����x=18��
�൱ë����ﵽ30��Ԫʱ��ֱ�����۵�A����÷��18��
��3���⣺��ù�˾��132��Ԫ��������m����÷������A����÷Ϊx�֣�B����÷Ϊ��m��x���֣�
�������Ϊ3m��Ԫ��A����÷�ӹ��ɱ�Ϊx��Ԫ��B����÷�ӹ��ɱ�Ϊ[12+3��m��x��]��Ԫ��
��3m+x+[12+3��m��x��]=132������ã�x=3m��60��
�ٵ�2��x��8ʱ��
wA=x����x+14����x=��x2+13x��
wB=9��m��x����[12+3��m��x��]=6m��6x��12
��w=wA+wB��3��m
=����x2+13x��+��6m��6x��12����3m
=��x2+7x+3m��12��
��3m=x+60����ã�w=��x2+8x+48=����x��4��2+64
�൱x=4ʱ�������ë����64��Ԫ��
��ʱm= ![]() ��m��x=
��m��x= ![]() ��
��
�ڵ�x��8ʱ��
wA=6x��x=5x��
wB=9��m��x����[12+3��m��x��]=6m��6x��12
��w=wA+wB��3��m
=��5x��+��6m��6x��12����3m
=��x+3m��12��
��3m=x+60����ã�w=48
�൱x��8ʱ�������ë����48��Ԫ��
����������������÷�� ![]() �֣�����A����÷4�֣�B��
�֣�����A����÷4�֣�B�� ![]() �֣���˾�ܹ�������ë�������ë����Ϊ64��Ԫ��
�֣���˾�ܹ�������ë�������ë����Ϊ64��Ԫ��
����������1������һ���ֶκ������ֱ�����亯����ϵʽ����2���ٵ�2��x��8ʱ����x��8ʱ���ֱ����w����x�ı���ʽ��ע��w=���������멁��Ӫ�ܳɱ�=wA+wB��3��20�������ù�˾�����30��Ԫë����30��Ԫ���������õı���ʽ�����A����÷����������3�������Ƿ���������⣬��Ͷ��Ϊ132��Ԫ�����132��Ԫ����������÷�ķ���+A����÷�ӹ��ɱ�+B����÷�ӹ��ɱ�����������m����÷������A����÷Ϊx�֣�B����÷Ϊ��m��x���֣��ֱ������2��x��8ʱ����x��8ʱw����x�ı���ʽ�����ֱ���������ֵ��


 �������ͬ����ϰϵ�д�
�������ͬ����ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����γ̸ĸijУ������չУ���γ̽��裬�ƻ���������ѧ���͡�������ѧʵ�顱���������赸���͡��ֹ���֯���ȶ�����ţ�Ҫ��ÿλѧ��������ѡ������һ�����ţ�Ϊ�ˣ���������˱�У���꼶����ѧ��ѡ�����ŵ����������������Ƴ�����ͳ��ͼ��������������
ѡ������ | ��ռ�ٷֱ� |
��ѧ���� | a |
��ѧʵ�� | 35% |
�����赸 | b |
�ֹ���֯ | 10% |
���� | c |
����ͳ��ͼ���е���Ϣ������������⣺
��1���ε����ѧ����������a��b��c��ֵ��
��2��������ͳ��ͼ����������
��3������У����1200��ѧ�����Թ���ȫУѡ��ѧʵ�顱���ŵ�ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ˣ�1������λͬѧ�μ�ѧУ�ٰ����ѧ�����������Ծ��й���20���⣬�涨ÿ���Ե�5�֣������2�֣�δ���0�֣�����A��B��C��D��E��λͬѧ�������ֱ����䲢��¼���Լ��Ĵ��������Eͬѧֻ�ǵ���7����δ�𣩣��������±�
����ͬѧ | ������� | ������� | δ������ |
A | 19 | 0 | 1 |
B | 17 | 2 | 1 |
C | 15 | 2 | 3 |
D | 17 | 1 | 2 |
E | / | / | 7 |
��1������������Ϣ����A��B��C��D��λͬѧ�ɼ���ƽ���֣�
��2������֪A��B��C��D��E��λͬѧ�ɼ��ֱ���95�֣�81�֣�64�֣�83�֣�58�֣� ����Eͬѧ�Ĵ�������ʹ��������
�ھ����㣬A��B��C��D��λͬѧʵ�ʳɼ���ƽ������80.75�֣��루1������õ�ƽ���ֲ����������������һλͬѧ�Ǵ����Լ��Ĵ����������ָ����λͬѧ�Ǵ��ˣ���д������ʵ�ʴ��������ֱ��д���𰸼��ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ���AC=4cm���������ŶԽ���AC����ƽ��1cm�õ�����EFGH����ͼ����Ӱ����ͼ�ε�������ı���EMCN�����֮��Ϊ�� �� 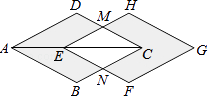
A.4��3
B.3��2
C.14��9
D.17��9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊn��������OABC�ı�OA��OC���������ϣ���A1 �� A2 �� ����An��1ΪOA��n�ȷֵ㣬��B1 �� B2 �� ����Bn��1ΪCB��n�ȷֵ㣬����A1B1 �� A2B2 �� ����An��1Bn��1 �� �ֱ�����y= ![]() ��x��0���ڵ�C1 �� C2 �� ����Cn��1 �� ��C15B15=16C15A15 �� ��n��ֵΪ �� ��nΪ��������
��x��0���ڵ�C1 �� C2 �� ����Cn��1 �� ��C15B15=16C15A15 �� ��n��ֵΪ �� ��nΪ�������� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������κ����Ķ�����ϵ��Ϊl����˶��κ����ɱ�ʾΪy=x2+px+q�����dz�[p��q]Ϊ�˺��������������纯��y=x2+2x+3����������[2��3]��
��1����һ��������������Ϊ[��2��1]����˺���ͼ��Ķ������꣮
��2��̽���������⣺ ����һ��������������Ϊ[4����1]�����˺�����ͼ��������ƽ��1����λ��������ƽ��1����λ����õ���ͼ���Ӧ�ĺ�������������
����һ��������������Ϊ[2��3]���ʴ˺�����ͼ��������ƽ�ƣ�����ʹ�õ���ͼ���Ӧ�ĺ�����������Ϊ[3��4]��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+c��ͼ���A��2��0����B��0����1����C��4��5�����㣮 
��1������κ����Ľ���ʽ��
��2������κ�����ͼ����x�����һ������ΪD�����D�����ꣻ
��3����ͬһ����ϵ�л���ֱ��y=x+1����д����x��ʲô��Χ��ʱ��һ�κ�����ֵ���ڶ��κ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����Dλ�ڡ�ABC��AC�ϣ���֪AB��AD��AC�ı������ 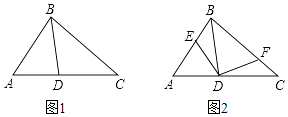
��1����֤����ACB=��ABD��
��2�����е�E��F�ֱ��ڱ�AB��BC����ͼ2�������EDF=��A+��C����AB=4��BC=5��CA=6ʱ����֤��DE=DF��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com