
【题目】已知射线AB∥射线CD,P为一动点,AE平分∠PAB,CE平分∠PCD,且AE与CE相交于点E.

(1)在图1中,当点P运动到线段AC上时,∠APC=180°.
①直接写出∠AEC的度数;②求证:∠AEC=∠EAB+∠ECD;
(2)当点P运动到图2的位置时,猜想∠AEC与∠APC之间的关系,并加以说明;
(3)当点P运动到图3的位置时,(2)中的结论是否还成立?若成立,请说明理由;若不成立,请写出∠AEC与∠APC之间的关系,并加以证明。
【答案】(1))①∠AEC=90°②见解析;(2)∠AEC=![]() ∠APC, 理由见解析;(3)不成立,∠AEC=180
∠APC, 理由见解析;(3)不成立,∠AEC=180![]() ∠APC ,理由见解析
∠APC ,理由见解析
【解析】
(1)①由平行线的性质可得出∠PAB+∠PCD=180°,进而可得出∠AEC的度数;
②在图1中,过E作EF∥AB,根据平行线的性质可得出∠AEF=∠EAB、∠CEF=∠ECD,进而即可证出∠AEC=∠AEF+∠CEF=∠EAB+∠ECD;
(2)猜想:∠AEC=![]() ∠APC,由角平分线的定义可得出∠EAB=
∠APC,由角平分线的定义可得出∠EAB=![]() ∠PAB、∠ECD=
∠PAB、∠ECD=![]() ∠PCD,由(1)可知∠AEC=∠EAB+∠ECD、∠APC=∠PAB+∠PCD,进而即可得出∠AEC=
∠PCD,由(1)可知∠AEC=∠EAB+∠ECD、∠APC=∠PAB+∠PCD,进而即可得出∠AEC=![]() (∠PAB+∠PCD)=
(∠PAB+∠PCD)=![]() ∠APC;
∠APC;
(3)在图3中,(2)中的结论不成立,而是满足∠AEC=180°-![]() ∠APC,过P作PQ∥AB,由平行线的性质可得出∠PAB+∠APQ=180°、∠CPQ+∠PCD=180°,进而可得出∠PAB+∠PCD=360°-∠APC,再由角平分线的定义可得出∠EAB=
∠APC,过P作PQ∥AB,由平行线的性质可得出∠PAB+∠APQ=180°、∠CPQ+∠PCD=180°,进而可得出∠PAB+∠PCD=360°-∠APC,再由角平分线的定义可得出∠EAB=![]() ∠PAB、∠ECD=
∠PAB、∠ECD=![]() ∠PCD,结合(1)的结论即可证出∠AEC=180°-
∠PCD,结合(1)的结论即可证出∠AEC=180°-![]() ∠APC.
∠APC.
(1)①∵AB∥CD,
∴∠PAB+∠PCD=180°,
∴∠AEC=90°;
②证明:在图1中,过E作EF∥AB,则∠AEF=∠EAB.
∵AB∥CD,
∴EF∥CD,
∴∠CEF=∠ECD.
∴∠AEC=∠AEF+∠CEF=∠EAB+∠ECD.
(2)猜想:∠AEC=![]() ∠APC,理由如下:
∠APC,理由如下:
∵AE、CE分别平分∠PAB和∠PCD,
∴∠EAB=![]() ∠PAB,∠ECD=
∠PAB,∠ECD=![]() ∠PCD.
∠PCD.
由(1)知∠AEC=∠EAB+∠ECD,∠APC=∠PAB+∠PCD,
∴∠AEC=![]() ∠PAB+
∠PAB+![]() ∠PCD=
∠PCD=![]() (∠PAB+∠PCD)=
(∠PAB+∠PCD)= ![]() ∠APC.
∠APC.
(3)在图3中,(2)中的结论不成立,而是满足∠AEC=180![]() ∠APC,
∠APC,

其证明过程是:
过P作PQ∥AB,则∠PAB+∠APQ=180°.
∵AB∥CD,
∴PQ∥CD,
∴∠CPQ+∠PCD=180.
∴∠PAB+∠APQ+∠CPQ+∠PCD=360°,即∠PAB+∠PCD=360°∠APC.
∵AE、CE分别平分∠PAB和∠PCD,
∴∠EAB=![]() ∠PAB,∠ECD=
∠PAB,∠ECD=![]() ∠PCD.
∠PCD.
由(1)知∠AEC=∠EAB+∠ECD,
∴∠AEC=![]() ∠PAB+
∠PAB+![]() ∠PCD=
∠PCD=![]() (∠PAB+∠PCD)= 180°-
(∠PAB+∠PCD)= 180°-![]() ∠APC.
∠APC.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】在2016年“双十一”期间,某快递公司计划租用甲、乙两种车辆快递货物,从货物量来计算:若租用两种车辆合运,10天可以完成任务;若单独租用乙种车辆,完成任务的天数是单独租用甲种车辆完成任务天数的2倍.
(1)求甲、乙两种车辆单独完成任务分别需要多少天?
(2)已知租用甲、乙两种车辆合运需租金65000元,甲种车辆每天的租金比乙种车辆每天的租金多1500元,试问:租甲和乙两种车辆、单独租甲种车辆、单独租乙种车辆这三种租车方案中,哪一种租金最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆运动(含P、Q两点),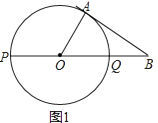
(1)当线段AB所在的直线与圆O相切时,求弧AQ的长(图1);
(2)若∠AOB=120°,求AB的长(图2);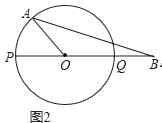
(3)如果线段AB与圆O有两个公共点A、M,当AO⊥PM于点N时,求tan∠MPQ的值(图3).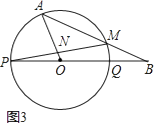
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
(1)写出点A、B的坐标:A( , )、B( , );
(2)求△ABC的面积;
(3)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,画出△A′B′C′,写出A′、B′、C′三个点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
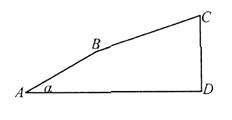
【题目】如图,小刚从点 ![]() 出发,沿着坡度为
出发,沿着坡度为 ![]() 的斜坡向上走了650米到达点
的斜坡向上走了650米到达点 ![]() ,且
,且 ![]() .
.
(1)则他上升的高度是 米 ;
(2)然后又沿着坡度为 ![]() 的斜坡向上走了1000米达到点
的斜坡向上走了1000米达到点 ![]() .问小刚从
.问小刚从 ![]() 点到
点到 ![]() 点上升的高度
点上升的高度 ![]() 是多少米(结果保留根号)?
是多少米(结果保留根号)?
查看答案和解析>>
科目:初中数学 来源: 题型:
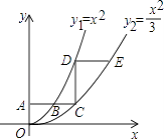
【题目】如图,平行于x轴的直线AC分别交函数y1=x2(x≥0)与y2= ![]() (x≥0)的图象于B、C两点,过点C作y轴的平行线交y1的图象于点D,直线DE∥AC,交y2的图象于点E,则
(x≥0)的图象于B、C两点,过点C作y轴的平行线交y1的图象于点D,直线DE∥AC,交y2的图象于点E,则 ![]() = .
= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由![]() 个同样大小的小正方体搭成的物体.
个同样大小的小正方体搭成的物体.
(1)请画阴影分别表示从正面、上面观察得到的平面图形的示意图;
(2)分别从正面、上面观察这个图形,得到的平面图形不变的情况下,你认为最多还可以添加 个小正方体.



从正面看 从上面看
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com