
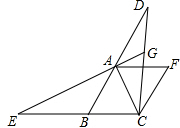
 如图,在?ABCF中,∠ABC=60°,AB=BC,延长BA到D,延长CB到E,使BE=AD,连结DC,交AF于H,连结EA并延长交CD于点G.
如图,在?ABCF中,∠ABC=60°,AB=BC,延长BA到D,延长CB到E,使BE=AD,连结DC,交AF于H,连结EA并延长交CD于点G.分析 (1)根据等边三角形的判定与性质,可得AC与AB的关系,根据等角的补角相等,可得∠ABE=∠CAD=120°,再根据全等三角形的判定与性质,可得答案;
(2)根据全等三角形的性质,可得∠AEB=∠D,根据三角形外角的性质,可得∠EGC=∠D+∠DAG,∠AEB+∠BEA=∠ABC,再根据等量代换,可得答案;
(3)根据平行线的性质,可得∠DAH,根据等腰三角形的性质,可得∠E,根据三角形外角的性质,可得∠AHC的度数,根据勾股定理,可得CD的长,CG的长,根据线段的和差,可得答案.
解答 证明:(1)∵∠ABC=60°,AB=BC,
∴△ABC是等边三角形,
∴AB=AC,∠BAC=60°.
∴∠ABE=∠CAD=120°.
在△ABE和△CAD中,
$\left\{\begin{array}{l}{AB=AC}\\{∠ABE=∠CAD}\\{BE=AD}\end{array}\right.$
∴△AEB≌△CDA(SAS),
∴EA=DC;
(2)∵△AEB≌△CDA,
∴∠AEB=∠D.
∵∠EGC=∠D+∠DAG,∠DAG=∠BAE,
∴∠EGC=∠AEB+∠BEA=∠ABC=60°;
(3)∵∠ABC=60°,AF∥BC,
∴∠DAH=60°.
∵BE=AB=2,
∴∠E=∠BAE.
∵∠E+∠BAE=60°,
∴∠E=30°.
∴∠D=30°.
∴∠AHC=∠DAH+∠D=60°+30°=90°.
∵AF∥BC,∠AHC=90°,
∴∠BCD=90°.
∵BD=BA+AD=2+2=4,BC=2,
∴CD=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
设CG=x,∵∠E=30°,
∴EG=2x,
∴(2x)2=x2+42.
∴x=$\frac{4\sqrt{3}}{3}$.
∴DG=CD-CG=2$\sqrt{3}$-$\frac{4\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$.
点评 本题考查了平行四边形的性质,利用等边三角形的性质得出AC与AB的关系是解题关键;利用三角形外角的性质得出∠EGC=∠D+∠DAG,∠AEB+∠BEA=∠ABC是解题关键;利用勾股定理得出CD,CG的长是解题关键.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,已知在△ABC中,∠A=90°
如图,已知在△ABC中,∠A=90°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-1,3)、B(n,-1).
如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-1,3)、B(n,-1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①PA平分∠BAC,②AS=AR,③QP∥AR,④△BRP≌△CSP中,一定成立的是①②③④(填写编号即可)
在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①PA平分∠BAC,②AS=AR,③QP∥AR,④△BRP≌△CSP中,一定成立的是①②③④(填写编号即可)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com