
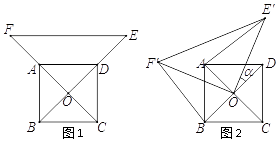
【题目】如图1,已知 ![]() 为正方形
为正方形 ![]() 的中心,分别延长
的中心,分别延长 ![]() 到点
到点 ![]() ,
, ![]() 到点
到点 ![]() ,使
,使 ![]() ,
, ![]() ,连结
,连结 ![]() ,将△
,将△ ![]() 绕点
绕点 ![]() 逆时针旋转
逆时针旋转 ![]() 角得到△
角得到△ ![]() (如图2).连结
(如图2).连结 ![]() 、
、 ![]() .
.
(Ⅰ)探究 ![]() 与
与 ![]() 的数量关系,并给予证明;
的数量关系,并给予证明;
(Ⅱ)当 ![]() ,
, ![]() 时,求:
时,求:
① ![]() 的度数;
的度数;
② ![]() 的长度.
的长度.
【答案】解:如图:
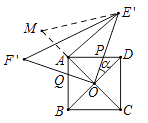
(Ⅰ)∵正方形ABCD中,OA=OD=OB,
又∵OF=2OA,OE=2OD,
∴OE=OF,则OE′=OF′,
在△AOE′和△BOF′中,
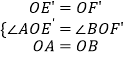
∴△AOE′≌△BOF′
∴AE′=BF′;
(Ⅱ)①延长OA到M,使AM=OA,则OM=OE′.
∵正方形ABCD中,∠AOD=90°,
∴∠AOE′=90°﹣30°=60°,
∴△OME′是等边三角形,
又∵AM=OA,
∴AE′⊥OM,
则∠E′AO=90°,
∴∠AOE′=90°﹣α=60°,
∴在直角△AOE′中,∠AE′O=90°﹣∠AOE′=30°;
②∵∠AOE′=90°﹣α=60°,∠E′OF′=90°,
∴∠AOF′=30°,
又∵∠AOB=90°,
∴∠BOF′=60°,
又∵等腰直角△AOB中,OB= ![]() AB=
AB= ![]() ,
,
∴在Rt△ABE'中得到AE'= ![]() OA=
OA= ![]() ,
,
又BF'=AE'
∴BF′= ![]() .
.
【解析】(Ⅰ)由正方形的性质可证明△AOE′≌△BOF′,进而得出结论;
(Ⅱ)①延长OA到M,使AM=OA,则OM=OE′.由正方形的性质和已知可得△OME′是等边三角形,进而在直角△AOE′中可求出∠AE′O的度数;
②先求出∠BOF′=60°,在等腰直角△AOB中利用三角函数可求出OB的长,在Rt△ABE'中利用三角函数可求出AE′的长,从而可得BF′的长.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.
(1)请在图中画出平移后的△A′B′C′,
(2)再在图中画出△A′B′C′的高C′D′,并求出△ABC在整个平移过程中线段AC扫过的面积为________.
(3)能使S△MBC=S△ABC的格点M共有_______个(点M异于点A)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠A是锐角,E为边AD上一点,△ABE沿着BE折叠,使点A的对应点F恰好落在边CD上,连接EF,BF,给出下列结论:
①若∠A=70°,则∠ABE=35°;②若点F是CD的中点,则S△ABE![]() S菱形ABCD
S菱形ABCD
下列判断正确的是( )

A. ①,②都对B. ①,②都错C. ①对,②错D. ①错,②对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,三角形ABC的顶点坐标分别为![]() ,
,![]() ,
,![]() ,把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形
,把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形![]() .
.
(1)画出三角形ABC和平移后![]() 的图形;
的图形;
(2)写出三个顶点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(3)求三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,点E是BD上一点,过点E作EF⊥AE交射线CB于点F,连结CE.
(1)已知点F在线段BC上.
①若AB=BE,求∠DAE度数;
②求证:CE=EF;
(2)已知正方形边长为2,且BC=2BF,请直接写出线段DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过对某校七年级学生体育选修课程的统计,得到以下信息:
①参加选课的总人数为300;
②参加选课的学生在“足球、篮球、排球、乒乓球”中都选择了一门;
③选足球和选排球的人数共占总人数的50%;选乒乓球的人数是选排球人数的2倍;
选足球和选篮球的人数共占总人数的85%.
设选足球的人数为x,选排球的人数为y,试列出二元一次方程组,分别求出选择足球、篮球、排球、乒乓球各门课程的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】真假命题的思考.
一天,老师在黑板上写下了下列三个命题:
①垂直于同一条直线的两条直线平行;
②若![]() ,则
,则![]()
③若![]() 和
和![]() 的两边所在直线分别平行,则
的两边所在直线分别平行,则![]() .
.
小明和小丽对话如下,
小明:“命题①是真命题,好像可以证明.”
小丽:“命题①是假命题,好像少了一些条件.”
(1)结合小明和小丽的对话,谈谈你的观点.如果你认为是真命题,请证明:如果你认为是假命题,请增加一个适当的条件,使之成真命题.
(2)请在命题②、命题③中选一个,如果你认为它是真命题,请证明:如果你认为它是假命题,请举出反例.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下表中的二次函数 ![]() 的自变量x与函数y的对应值,可判断二次函数的图像与x轴( )
的自变量x与函数y的对应值,可判断二次函数的图像与x轴( )
A.只有一个交点
B.有两个交点,且它们分别在y轴两侧
C.有两个交点,且它们均在y轴同侧
D.无交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.

解:∵∠A=∠F(已知)
∴AC∥DF( )
∴∠D=∠ ( )
又∵∠C=∠D(已知)
∴∠1=∠C(等量代换)
∴BD∥CE( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com