
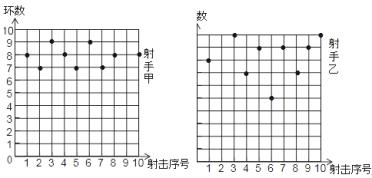
【题目】甲、乙两名射手在相同条件下打靶,射中的环数如图所示,利用图中提供的信息,解答下列问题:
(1)分别求甲、乙两名射手中环数的众数和平均数;
(2)如果从甲、乙两名射手中选一名去参加射击比赛,你选谁去?为什么?
【答案】(1)甲射手所中环数的众数为8;乙射手所中环数的众数为9;甲射手所中环数的平均数为![]() ;乙射手所中环数的平均数为
;乙射手所中环数的平均数为![]() ;(2)选乙去.
;(2)选乙去.
【解析】
(1)分别根据众数的定义与平均数公式计算即可;
(2)分别计算甲、乙两名射手的方差,然后根据方差小的数据的比较稳定即可选出哪个选手去参加比赛.
解:(1)甲射手所中环数为:8,7,9,8,7,9,7,8,8.出现次数最多的是8,所以甲射手所中环数的众数为8;
乙射手所中环数为:8,10,7,9,5,9,7,9,10.出现次数最多的是9,所以乙射手所中环数的众数为:9;
![]() =
=![]() ×(7×3+8×4+9×2)=
×(7×3+8×4+9×2)=![]() ;
;
![]() =
=![]() ×(5+7×2+8+9×3+10×2)=
×(5+7×2+8+9×3+10×2)=![]() ;
;
(2)S甲2=![]() [3×(7﹣
[3×(7﹣![]() )2+4×(8﹣
)2+4×(8﹣![]() )2+2×(9﹣
)2+2×(9﹣![]() )2]=
)2]=![]() ;
;
S乙2=![]() ×[(5﹣
×[(5﹣![]() )2+2×(7﹣
)2+2×(7﹣![]() )2+(8﹣
)2+(8﹣![]() )2+3×(9﹣
)2+3×(9﹣![]() )2+2×(10﹣
)2+2×(10﹣![]() )2]=
)2]=![]() .
.
∵S甲2>S乙2 ,
∴成绩最稳定的选手是乙.
∴如果从甲、乙两名射手中选一名去参加射击比赛,选乙去.


科目:初中数学 来源: 题型:
【题目】计算:
(1)(5mn2﹣4m2n)(﹣2mn)
(2)(x+7)(x﹣6)﹣(x﹣2)(x+1)
(3) (-![]() )2 016×161 008;
)2 016×161 008;
【答案】(1)﹣10m2n3+8m3n2;(2)2x﹣40;(3)1.
【解析】试题分析:(1)原式利用单项式乘以多项式法则计算即可得到结果;
(2)原式两项利用多项式乘以多项式法则计算,去括号合并即可得到结果;
(3)先根据幂的乘方的逆运算,把(-![]() )2 016化为(
)2 016化为(![]() )1008,再根据积的乘方的逆运算计算即可.
)1008,再根据积的乘方的逆运算计算即可.
试题解析:(1)原式=(5mn2)(﹣2mn)+(﹣4m2n)(﹣2mn)=﹣10m2n3+8m3n2;
(2)原式=x2﹣6x+7x﹣42﹣x2﹣x+2x+2=2x﹣40.
(3)原式=(![]() )1008×161 008=(
)1008×161 008=(![]() ×16)1 008=1.
×16)1 008=1.
【题型】解答题
【结束】
19
【题目】如图,方格图中每个小正方形的边长为1,点A、B、C都是格点.
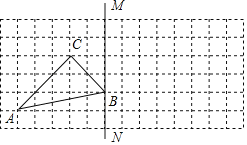
(1)画出△ABC关于直线BM对称的△A1B1C1;
(2)写出AA1的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABE=∠ACD=Rt∠,AE=AD,∠ABC=∠ACB.求证:∠BAE=∠CAD.
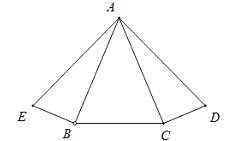
请补全证明过程,并在括号里写上理由.
证明:在△ABC中,
∵∠ABC=∠ACB
∴AB= ( )
在Rt△ABE和Rt△ACD中,
∵ =AC, =AD
∴Rt△ABE≌Rt△ACD( )
∴∠BAE=∠CAD( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A点坐标为(2,4),B点坐标为(﹣3,﹣2),C点坐标为(3,1).
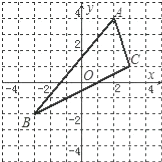
(1)在图中画出△ABC关于y轴对称的△A′B′C′(不写画法),并写出点A′,B′,C′的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一根24cm的筷子置于底面直径为15cm,高为8cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是( )
A. h≤17 B. h≥8 C. 15≤h≤16 D. 7≤h≤16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com