Question

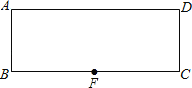
【题目】在矩形纸片ABCD中，AB=8，BC=20，F为BC的中点，沿过点F的直线翻折，使点B落在边AD上，折痕交矩形的一边于G，则折痕FG= ．

Answer 1

【答案】5或4．

【解析】

试题分析：过F作FE⊥AD于E，可得出四边形ABFE为矩形，利用矩形的性质得到AE=BF，AB=EF，分两种情况考虑：（i）当G在AB上，B′落在AE上时，如图1所示，由折叠的性质得到B′F=BF，BG=B′G，在直角三角形EFB′中，利用勾股定理求出B′E的长，由AE﹣B′E求出AB′的长，设AG=x，由AB﹣AG表示出BG，即为B′G，在直角三角形AB′G中，利用勾股定理列出关于x的方程，求出方程的解得到x的值，确定出AG的长，进而求出BG的长，在直角三角形GBF中，利用勾股定理即可求出折痕FG的长；（ii）当G在AE上，B′落在ED上，如图2所示，同理求出B′E的长，设A′G=AG=y，由AE+B′E﹣AG表示出GB′，在直角三角形A′B′G中，利用勾股定理列出关于y的方程，求出方程的解得到y的值，求出AG的长，由AE﹣AG求出GE的长，在直角三角形GEF中，利用勾股定理即可求出折痕FG的长，综上，得到所有满足题意的折痕FG的长．

解：分两种情况考虑：

（i）如图1所示，过F作FE⊥AD于E，G在AB上，B′落在AE上，可得四边形ABFE为矩形，

∴EF=AB=8，AE=BF，

又BC=20，F为BC的中点，

∴由折叠可得：B′F=BF=BC=10，

在Rt△EFB′中，根据勾股定理得：B′E==6，

∴AB′=AE﹣B′E=10﹣6=4，

设AG=x，则有GB′=GB=8﹣x，

在Rt△AGB′中，根据勾股定理得：GB′2=AG2+AB′2，

即（8﹣x）2=x2+42，

解得：x=3，

∴GB=8﹣3=5，

在Rt△GBF中，根据勾股定理得：GF==5；

（ii）如图2所示，过F作FE⊥AD于E，G在AE上，B′落在ED上，可得四边形ABFE为矩形，

∴EF=AB=8，AE=BF，

又BC=20，F为BC的中点，

∴由折叠可得：B′F=BF=BC=10，

在Rt△EFB′中，根据勾股定理得：B′E==6，

∴AB′=AE+B′E=10+6=16，

设AG=A′G=y，则GB′=AB′﹣AG=AE+EB′﹣AG=16﹣y，A′B′=AB=8，

在Rt△A′B′G中，根据勾股定理得：A′G2+A′B′2=GB′2，

即y2+82=（16﹣y）2，

解得：y=6，

∴AG=6，

∴GE=AE﹣AG=10﹣6=4，

在Rt△GEF中，根据勾股定理得：GF==4，

综上，折痕FG=5或4．

故答案为：5或4．