
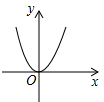 B.
B. C.
C.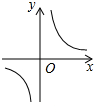 D.
D.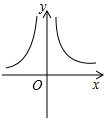
分析 (1)利用题中的新定义计算即可得到结果;
(2)分m大于0与小于0两种情况,利用题中的新定义计算即可求出m的值;
(3)分x大于0与x小于0两种情况化简函数解析式,做出函数图象即可.
解答 解:(1)根据题中的新定义得:3※7=$\frac{3}{7}$;
(2)当m>0时,已知等式变形得:$\frac{15}{m}$=$\frac{15}{4}$,即m=4;
当m<0时,已知等式变形得:-$\frac{15}{m}$=$\frac{15}{4}$,即m=-4;
(3)当x>0时,函数解析式为y=$\frac{4}{x}$,
当x<0时,函数解析式为y=-$\frac{4}{x}$,
图象大致为D.
故选:D.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:选择题
 如图,△ABC是边长为6cm的等边三角形,点P是AC边上一动点,由点A向点C运动(不与点A,C重合),点Q是CB延长线上一动点,与点P同时以相同的速度由点B向CB延长线方向运动(点Q不与点B重合),过点P作PE⊥AB于点E,连接PQ交AB于点D.则ED的长为( )
如图,△ABC是边长为6cm的等边三角形,点P是AC边上一动点,由点A向点C运动(不与点A,C重合),点Q是CB延长线上一动点,与点P同时以相同的速度由点B向CB延长线方向运动(点Q不与点B重合),过点P作PE⊥AB于点E,连接PQ交AB于点D.则ED的长为( )| A. | 2cm | B. | 3cm | ||
| C. | 4cm | D. | 缺少条件,无法求出 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
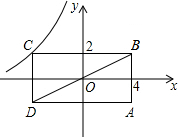 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=$\frac{k}{x}$的图象上,若点A的坐标为(4,-2),则k的值为-8.
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=$\frac{k}{x}$的图象上,若点A的坐标为(4,-2),则k的值为-8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,-3) | B. | (-2,-3) | C. | (2,3) | D. | (-1,-6) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,⊙C过原点O,交x轴于点A(2,0),交y轴于点B(0,$2\sqrt{3}}$).
如图,在直角坐标系中,⊙C过原点O,交x轴于点A(2,0),交y轴于点B(0,$2\sqrt{3}}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com