
【题目】如图,在Rt△ABC中,∠C=90°,点D在AB上,以AD为直径的⊙O与BC相交于点E,与AC相交于点F,AE平分∠BAC.
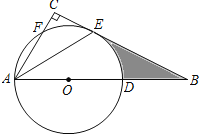
(1)求证:BC是⊙O的切线.
(2)若∠EAB=30°,OD=3,求图中阴影部分的面积.
(3)若AD=5,AE=4,求AF.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)如图,连结OE,由角平分线的定义可得∠CAE=∠EAD,由等腰三角形的性质可得∠EAD=∠OEA,即可证明∠OEA=∠CAE,可得OE//AC,根据平行线的性质可得∠OEB=∠C=90°,即可证明BC是⊙O的切线;(2)由角平分线的定义可得∠EOD=60°,即可得出∠B=30°,根据含30°角的直角三角形的性质可求出OB的长,利用勾股定理求出BE的长,根据S阴影=S△OEB-S扇形OED即可得答案;(3)如图,连接DE,EF,由AD是直径可得∠AED=90°,利用勾股定理可求出DE的长,由∠CAE=∠EAD,∠ACE=∠AED=90°可证明△ACE∽△AED,根据相似三角形的性质可求出AC、CE的长,∠ADE=∠AEC,由圆内接四边形的性质可得∠CFE=∠ADE,可得∠AEC=∠CFE,即可证明△CEF∽△CAE,根据相似三角形的性质可求出CF的长,根据AF=AC-CF可得答案.
(1)如图,连接OE,
∵AE平分∠BAC,
∴∠CAE=∠EAD,
∵OA=OE,
∴∠EAD=∠OEA,
∴∠OEA=∠CAE,
∴OE∥AC,
∴∠OEB=∠C=90°,
∴OE⊥BC,
∴BC是⊙O的切线.

(2)解:∵∠EAB=30°,AE平分∠BAC,
∴∠EOD=60°,
∴∠OEB=90°,
∴∠B=30°,
∴OB=2OE=2OD=6,
∴![]() ,
,
∴![]()
![]() ,
,
∴![]() .
.
(3)如图,连接DE,EF,
∵AD为⊙O的直径,
∴∠AED=90°,
∴![]() ,
,
∵AE平分∠BAC,
∴∠CAE=∠EAD,
又∵∠ACE=∠AED=90°,
∴△ACE∽△AED,
∴![]() ,∠ADE=∠AEC,
,∠ADE=∠AEC,
∴![]() ,
,![]()
∵四边形AFED为圆内接四边形,
∴∠AFE+∠ADE=180°,
∵∠CFE+∠AFE=180°,
∴∠CFE=∠ADE,
∴∠AEC=∠CFE,
∵∠FCE=∠ACE,
∴△CEF∽△CAE,
∴![]() ,
,
∴ ,
,
∴AF=AC﹣CF=![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】对于给定的图形G和点P,若点P可通过一次向上或向右平移n(n>0)个单位至图形G上某点P′,则称点P为图形G的“可达点”,特别地,当点P在图形G上时,点P为图形G的“可达点”.
(1)如图1,在平面直角坐标系xOy中,点A(1,1),B(2,1),
①在点O、A、B中,不是直线y=﹣x+2的“可达点”的是 ;
②若点A是直线l的“可达点”且点A不在直线l上,写出一条满足要求的直线l的表达式: ;
③若点A、B中有且仅有一点是直线y=kx+2的“可达点”,则k的取值范围是 .
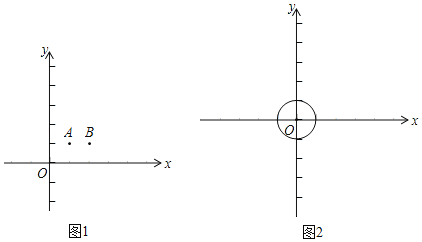
(2)如图2,在平面直角坐标系xOy中,⊙O的半径为1,直线l:y=﹣![]() x+b.
x+b.
①当b=﹣2时,若直线m上一点N(xN,yN)满足N是⊙O的“可达点”,直接写出xN的取值范围 ;
②若直线m上所有的⊙O的“可达点”构成一条长度不为0的线段,直接写出b的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在歌唱比赛中,一位歌手分别转动如下的两个转盘(每个转盘都被分成3等份)一次,根据指针指向的歌曲名演唱两首曲目.

(1)转动转盘①时,该转盘指针指向歌曲“3”的概率是 ;
(2)若允许该歌手替换他最不擅长的歌曲“3”,即指针指向歌曲“3”时,该歌手就选择自己最擅长的歌曲“1”, 请用树形图或列表法中的一种,求他演唱歌曲“1”和“4”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了准备科技节创意销售,宏帆初2018级某同学到批发市场购买了一些甲、乙两种型号的小元件,甲型小元件的单价是6元,乙型小元件的单价是3元,该同学的创意作品每件需要的乙型小元件的个数是甲型小元件的个数的2倍,同时,为了控制成本,该同学购买小元件的总费用不超过480元.
(1)该同学最多可购买多少个甲型小元件?
(2)在该同学购买甲型小元件最多的前提下,用所购买的甲、乙两种型号的小元件全部制作成创意作品,在制作中其他费用共花520元,销售当天,该同学在成本价(购买小元件的费用+其他费用)的基础上每件提高2a%(10<a<50)标价,但无人问津,于是该同学在标价的基础上降低a%出售,最终,在活动结束时作品全部卖完,这样,该同学在本次活动中赚了![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com