搜索
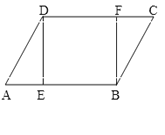
【题目】如图，在□ABCD中，E、F分别是AB、DC边上的点，且AE=CF，
（1）求证：
≌
.
（2）若
DEB=90
，求证四边形DEBF是矩形.
参考答案：
【答案】（1）利用SAS证明；（2）证明见解析.
【解析】
试题此题考查了平行四边形的判定与性质、矩形的判定以及全等三角形的判定与性质．注意有一个角是直角的平行四边形是矩形，首先证得四边形ABCD是平行四边形是关键．（1）由在□ABCD中，AE=CF，可利用SAS判定△ADE≌△CBF．（2）由在ABCD中，且AE=CF，利用一组对边平行且相等的四边形是平行四边形，可证得四边形DEBF是平行四边形，又由∠DEB=90°，可证得四边形DEBF是矩形．
试题解析：（1）∵四边形ABCD是平行四边形，
∴AD=CB，∠A=∠C，
在△ADE和△CBF中，
，
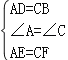∴△ADE≌△CBF（SAS）．
（2）∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，
∵AE=CF，∴BE=DF，
∴四边形ABCD是平行四边形，
∵∠DEB=90°，∴四边形DEBF是矩形．
故答案为（1）利用SAS证明；（2）证明见解析.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，AB=8，BC=6，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，且OE=OD，则AP的长为 ( ) ．
A.4.8B.3
C.5D.3
-
科目： 来源： 题型：
查看答案和解析>>【题目】某博物馆每周都吸引大量中外游客前来参观，如果游客过多，对馆中的珍贵文物会产生不利影响，但同时考虑到文物的修缮和保存费用问题，还要保证一定的门票收入，因此，博物馆采取了涨浮门票价格的方法来控制参观人数，在该方法实施过程中发现：每周参观人数与票价之间存在着如图所示的一次函数关系．在这种情况下，如果要保证每周
万元的门票收入，那么每周应限定参观人数是多少？门票价格应是多少．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某化妆品店老板到厂家选购A、B两种品牌的化妆品，若购进A品牌的化妆品5套，B品牌的化妆品6套，需要950元；若购进A品牌的化妆品3套，B品牌的化妆品2套，需要450元．
求A、B两种品牌的化妆品每套进价分别为多少元？
若销售1套A品牌的化妆品可获利30元，销售1套B品牌的化妆品可获利20元，根据市场需求，化妆品店老板决定，购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套，且B品牌化妆品最多可购进40套，这样化妆品全部售出后，可使总的获利不少于1200元，问有几种进货方案？如何进货？ -
科目： 来源： 题型：
查看答案和解析>>【题目】现有一副直角三角板（角度分别为30°、60°、90°和45°、45°、90°），如图(1)所示，其中一块三角板的直角边AC垂直于数轴，AC的中点过数轴原点O，AC＝8，斜边AB交数轴于点G，点G对应数轴上的数是4；另一块三角板的直角边AE交数轴于点F，斜边AD交数轴于点H．
（1）如果△AGH的面积是10，△AHF的面积是8，则点F对应的数轴上的数是 ，点H对应的数轴上的数是 ；
（2）如图(2)，设∠AHF的平分线和∠AGH的平分线交于点M，若∠HAO＝a，试用a来表示∠M的大小：（写出推理过程）
（3）如图(2)，设∠AHF的平分线和∠AGH的平分线交于点M，设∠EFH的平分线和
∠FOC的平分线交于点N，求∠N＋∠M的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（7分）如图，平行四边形ABCD中，AB=3cm，BC=5cm，∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连接CE，DF．
（1）求证：四边形CEDF是平行四边形；
（2）①当AE= cm时，四边形CEDF是矩形；
②当AE= cm时，四边形CEDF是菱形；（直接写出答案，不需要说明理由）
-
科目： 来源： 题型：
查看答案和解析>>【题目】图①是一个三角形，分别连接这个三角形三边的中点得到图②；再分别连接图②中间小三角形三边的中点，得到图③.
（1）图②有_____个三角形；图③有_____个三角形.
（2）按上面的方法继续下去，第
个图形中有 个三角形？
相关试题
