
【题目】阅读材料:基本不等式![]() ≤
≤![]() (a>0,b>0),当且仅当a=b时,等号成立.其中我们把
(a>0,b>0),当且仅当a=b时,等号成立.其中我们把![]() 叫做正数a、b的算术平均数,
叫做正数a、b的算术平均数,![]() 叫做正数a、b的几何平均数,它是解决最大(小)值问题的有力工具.
叫做正数a、b的几何平均数,它是解决最大(小)值问题的有力工具.
例如:在x>0的条件下,当x为何值时,x+![]() 有最小值,最小值是多少?
有最小值,最小值是多少?
解:∵x>0,![]() >0∴
>0∴![]() ≥
≥![]() 即是x+
即是x+![]() ≥2
≥2![]()
∴x+![]() ≥2
≥2
当且仅当x=![]() 即x=1时,x+
即x=1时,x+![]() 有最小值,最小值为2.
有最小值,最小值为2.
请根据阅读材料解答下列问题
(1)若x>0,函数y=2x+![]() ,当x为何值时,函数有最小值,并求出其最小值.
,当x为何值时,函数有最小值,并求出其最小值.
(2)当x>0时,式子x2+1+![]() ≥2成立吗?请说明理由.
≥2成立吗?请说明理由.
科目:初中数学 来源: 题型:
【题目】为了响应政府“绿色出行”的号召,李华选择骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图像回答下列问题.
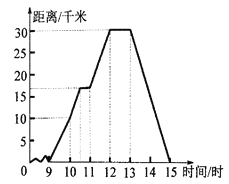
(1)李华到达离家最远的地方是几时?此时离家多远?
(2)李华返回时的速度是多少?
(3)李华全程骑车的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,请回答下列问题.
材料一:我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积,用现代式子表示即为: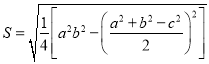 ①(其中
①(其中![]() 为三角形的三边长,
为三角形的三边长,![]() 为面积),而另一个文明古国古希腊也有求三角形面积的“海伦公式”;
为面积),而另一个文明古国古希腊也有求三角形面积的“海伦公式”;![]() ……②(其中
……②(其中![]() )
)
材料二:对于平方差公式:![]() 公式逆用可得:
公式逆用可得:![]() ,例:
,例:![]()
(1)若已知三角形的三边长分别为4,5,7,请分别运用公式①和公式②,计算该三角形的面积;
(2)你能否由公式①推导出公式②?请试试,写出推导过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是弧EB的中点,则下列结论:
①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )
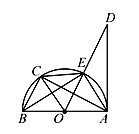
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A种产品用甲种原料9千克,乙种原料3千克,可获利700元;生产一件B种产品用甲种原料4千克,乙种原料10千克,可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润为y元,其中一种产品生产件数为x件,试写出y与x之间的函数关系式,并利用函数的性质说明那种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,⊙O过BC的中点D,且DE垂直AC于E.
(1)求证:AB=AC;
(2)求证:DE是⊙O的切线;
(3)若AB=13,BC=10,求DE的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有红球2个和白球2个,这些球除颜色外其余都相同,小明从袋子中任意摸出一球,记下颜色后不放回,若小明再从剩余的球中任取一球,请你用列表法或树状图的方法,求小明两次都摸出红球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com