
【题目】为了响应政府“绿色出行”的号召,李华选择骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图像回答下列问题.
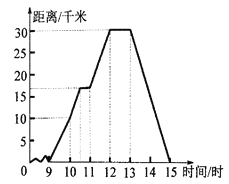
(1)李华到达离家最远的地方是几时?此时离家多远?
(2)李华返回时的速度是多少?
(3)李华全程骑车的平均速度是多少?
 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,一副三角板![]() 和
和![]() 拼合在一起,边
拼合在一起,边![]() 与
与![]() 重合,
重合,![]() ,
,![]() ,
,![]() ,
,![]() .当点
.当点![]() 从点
从点![]() 出发沿
出发沿![]() 向下滑动时,点
向下滑动时,点![]() 同时从点
同时从点![]() 出发沿射线
出发沿射线![]() 向右滑动.当点
向右滑动.当点![]() 从点
从点![]() 滑动到点
滑动到点![]() 时,连接
时,连接![]() ,则
,则![]() 的面积最大值为_______
的面积最大值为_______![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() ,
,![]() ,其中
,其中![]() ,
,![]() 满足
满足![]() ,点
,点![]() 为第三象限内一点.
为第三象限内一点.

(1)若![]() 到坐标轴的距离相等,
到坐标轴的距离相等,![]() ,且
,且![]() ,求
,求![]() 点坐标
点坐标
(2)若![]() 为
为![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() 的面积.
的面积.
(3)在(2)条件下,当![]() 时,在
时,在![]() 轴上有点
轴上有点![]() ,使得
,使得![]() 的面积是
的面积是![]() 的面积的2倍,请求出点
的面积的2倍,请求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万州某企业捐资购买了一批重120吨的物资支援某贫困乡镇,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下(假设每辆车均满载):甲载重5吨,运费400元/车,乙载重8吨,运费500元/车,丙载重10吨,运费600元/车,该公司计划用甲、乙、丙三种车型同时参与运送并完成任务,已知它们的总辆数为15辆,要使费用最省,所使用的甲、乙、丙三种车型的辆数分别是______。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批小家电,平均每天可售出20台,每台盈利40元.为了去库存,商场决定采取适当的降价措施.经调查发现,在一定范围内,小家电的单价每降5元,商场平均每天可多售出10台.
(1)若将这批小家电的单价降低x元,则每天的销售量是______台(用含x的代数式表示);
(2)如果商场通过销售这批小家电每天要盈利1250元,那么单价应降多少元?
(3)若这批小家电的单价有三种降价方式:降价10元、降价20元、降价30元,如果你是商场经理,你准备采取哪种降价方式?说说理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】统计七年级部分同学的跳高测试成绩,得到如下频率直方图(每组含前一个边界值,不含后一个边界值).

(1)参加测试的总人数是多少人?
(2)组距为多少?
(3)跳高成绩在![]() (含
(含![]() )以上的有多少人?占总人数的百分之几?
)以上的有多少人?占总人数的百分之几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:基本不等式![]() ≤
≤![]() (a>0,b>0),当且仅当a=b时,等号成立.其中我们把
(a>0,b>0),当且仅当a=b时,等号成立.其中我们把![]() 叫做正数a、b的算术平均数,
叫做正数a、b的算术平均数,![]() 叫做正数a、b的几何平均数,它是解决最大(小)值问题的有力工具.
叫做正数a、b的几何平均数,它是解决最大(小)值问题的有力工具.
例如:在x>0的条件下,当x为何值时,x+![]() 有最小值,最小值是多少?
有最小值,最小值是多少?
解:∵x>0,![]() >0∴
>0∴![]() ≥
≥![]() 即是x+
即是x+![]() ≥2
≥2![]()
∴x+![]() ≥2
≥2
当且仅当x=![]() 即x=1时,x+
即x=1时,x+![]() 有最小值,最小值为2.
有最小值,最小值为2.
请根据阅读材料解答下列问题
(1)若x>0,函数y=2x+![]() ,当x为何值时,函数有最小值,并求出其最小值.
,当x为何值时,函数有最小值,并求出其最小值.
(2)当x>0时,式子x2+1+![]() ≥2成立吗?请说明理由.
≥2成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
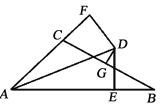
【题目】如图,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=11,AC=5,则BE=______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com