
【题目】统计七年级部分同学的跳高测试成绩,得到如下频率直方图(每组含前一个边界值,不含后一个边界值).

(1)参加测试的总人数是多少人?
(2)组距为多少?
(3)跳高成绩在![]() (含
(含![]() )以上的有多少人?占总人数的百分之几?
)以上的有多少人?占总人数的百分之几?
 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,可推得
,可推得![]() .理由如下:
.理由如下:
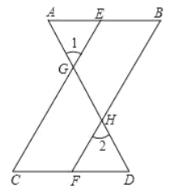
![]()
![]() (已知),
(已知),
且![]() (________)
(________)
![]()
![]() (等量代换)
(等量代换)
![]()
![]() (________)
(________)
![]()
![]() ________
________![]() (________)
(________)
又![]()
![]() (已知)
(已知)
![]()
![]() (等量代换)
(等量代换)
![]()
![]() (________)
(________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应政府“绿色出行”的号召,李华选择骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图像回答下列问题.
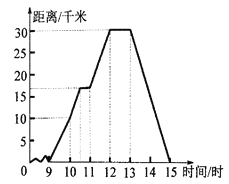
(1)李华到达离家最远的地方是几时?此时离家多远?
(2)李华返回时的速度是多少?
(3)李华全程骑车的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:如图1,在![]() 中,若
中,若![]() ,
,![]() .求
.求![]() 边上的中线
边上的中线![]() 的取值范围.小聪同学是这样思考的:延长
的取值范围.小聪同学是这样思考的:延长![]() 至
至![]() ,使
,使![]() ,连结
,连结![]() .利用全等将边
.利用全等将边![]() 转化到
转化到![]() ,在
,在![]() 中利用三角形三边关系即可求出中线
中利用三角形三边关系即可求出中线![]() 的取值范围.在这个过程中小聪同学证三角形全等用到的判定方法是__________;中线
的取值范围.在这个过程中小聪同学证三角形全等用到的判定方法是__________;中线![]() 的取值范围是__________.
的取值范围是__________.
(2)问题解决:如图2,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 边上,若
边上,若![]() .求证:
.求证:![]() .
.
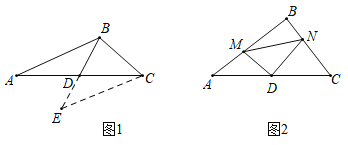
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,请回答下列问题.
材料一:我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积,用现代式子表示即为: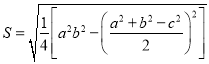 ①(其中
①(其中![]() 为三角形的三边长,
为三角形的三边长,![]() 为面积),而另一个文明古国古希腊也有求三角形面积的“海伦公式”;
为面积),而另一个文明古国古希腊也有求三角形面积的“海伦公式”;![]() ……②(其中
……②(其中![]() )
)
材料二:对于平方差公式:![]() 公式逆用可得:
公式逆用可得:![]() ,例:
,例:![]()
(1)若已知三角形的三边长分别为4,5,7,请分别运用公式①和公式②,计算该三角形的面积;
(2)你能否由公式①推导出公式②?请试试,写出推导过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A种产品用甲种原料9千克,乙种原料3千克,可获利700元;生产一件B种产品用甲种原料4千克,乙种原料10千克,可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润为y元,其中一种产品生产件数为x件,试写出y与x之间的函数关系式,并利用函数的性质说明那种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形第四个顶点坐标的是( )

A. (3,-1) B. (-1,-1) C. (1,1) D. (-2,-1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com