
ЁОЬтФПЁПЖдгкИјЖЈЕФЭМаЮGКЭЕуPЃЌШєЕуPПЩЭЈЙ§вЛДЮЯђЩЯЛђЯђгвЦНвЦnЃЈnЃО0ЃЉИіЕЅЮЛжСЭМаЮGЩЯФГЕуPЁфЃЌдђГЦЕуPЮЊЭМаЮGЕФЁАПЩДяЕуЁБЃЌЬиБ№ЕиЃЌЕБЕуPдкЭМаЮGЩЯЪБЃЌЕуPЮЊЭМаЮGЕФЁАПЩДяЕуЁБЃЎ
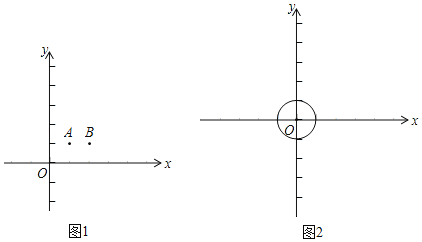
ЃЈ1ЃЉШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЕуAЃЈ1ЃЌ1ЃЉЃЌBЃЈ2ЃЌ1ЃЉЃЌ
ЂйдкЕуOЁЂAЁЂBжаЃЌВЛЪЧжБЯпyЃНЉx+2ЕФЁАПЩДяЕуЁБЕФЪЧЁЁ ЁЁЃЛ
ЂкШєЕуAЪЧжБЯпlЕФЁАПЩДяЕуЁБЧвЕуAВЛдкжБЯпlЩЯЃЌаДГівЛЬѕТњзувЊЧѓЕФжБЯпlЕФБэДяЪНЃКЁЁ ЁЁЃЛ
ЂлШєЕуAЁЂBжагаЧвНігавЛЕуЪЧжБЯпyЃНkx+2ЕФЁАПЩДяЕуЁБЃЌдђkЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЃЎ
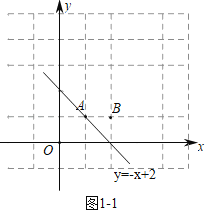
ЃЈ2ЃЉШчЭМ2ЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЁбOЕФАыОЖЮЊ1ЃЌжБЯпlЃКyЃНЉ![]() x+bЃЎ
x+bЃЎ
ЂйЕБbЃНЉ2ЪБЃЌШєжБЯпmЩЯвЛЕуNЃЈxNЃЌyNЃЉТњзуNЪЧЁбOЕФЁАПЩДяЕуЁБЃЌжБНгаДГіxNЕФШЁжЕЗЖЮЇЁЁ ЁЁЃЛ
ЂкШєжБЯпmЩЯЫљгаЕФЁбOЕФЁАПЩДяЕуЁБЙЙГЩвЛЬѕГЄЖШВЛЮЊ0ЕФЯпЖЮЃЌжБНгаДГіbЕФШЁжЕЗЖЮЇЁЁ ЁЁЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйBЃЛЂкyЃНЉx+3ЃЛЂлЉ1ЁмkЃМЉ![]() ЃЛЃЈ2ЃЉЂйЉ3
ЃЛЃЈ2ЃЉЂйЉ3![]() ЁмxNЁмЉ
ЁмxNЁмЉ![]() ЛђЉ1ЁмxNЁм1ЃЛЂкЉ1Љ
ЛђЉ1ЁмxNЁм1ЃЛЂкЉ1Љ![]() ЁмbЃМ
ЁмbЃМ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЂйИљОнЁАПЩДяЕуЁБЕФЖЈвхМДПЩНтОіЮЪЬтЃЎ
ЂкД№АИВЛЮЈвЛЃЌжБЯпдкЕуAЕФЩЯЗНМДПЩЃЎ
ЂлЧѓГіжБЯпyЃНkx+2ОЙ§ЕуAЛђЕуBЪБkЕФжЕМДПЩХаЖЯЃЎ
ЃЈ2ЃЉЂйЙ§ЕуЃЈ0ЃЌ1ЃЉКЭЕуЃЈ0ЃЌЉ1ЃЉзїxжсЕФЦНааЯпЗжБ№НЛжБЯпyЃНЉ![]() xЉ2гкN1ЃЈЉ3
xЉ2гкN1ЃЈЉ3![]() ЃЌ1ЃЉЃЌN2ЃЈЉ
ЃЌ1ЃЉЃЌN2ЃЈЉ![]() ЃЌЉ1ЃЉЃЌЙ§ЕуЃЈ1ЃЌ0ЃЉКЭЕуЃЈЉ1ЃЌ0ЃЉзїyжсЕФЦНааЯпЗжБ№НЛжБЯпyЃНЉ
ЃЌЉ1ЃЉЃЌЙ§ЕуЃЈ1ЃЌ0ЃЉКЭЕуЃЈЉ1ЃЌ0ЃЉзїyжсЕФЦНааЯпЗжБ№НЛжБЯпyЃНЉ![]() xЉ2гкN3ЃЈ1ЃЌЉ
xЉ2гкN3ЃЈ1ЃЌЉ![]() Љ2ЃЉЃЌN4ЃЈЉ1ЃЌ
Љ2ЃЉЃЌN4ЃЈЉ1ЃЌ![]() Љ2ЃЉЃЌгЩДЫМДПЩХаЖЯЃЎ
Љ2ЃЉЃЌгЩДЫМДПЩХаЖЯЃЎ
ЂкЕБN2гыN3жиКЯЃЌзјБъЮЊЃЈЉ1ЃЌЉ1ЃЉЪБЃЌЉ1ЃН![]() +bЃЌПЩЕУbЃНЉ1Љ
+bЃЌПЩЕУbЃНЉ1Љ![]() ЃЌЕБжБЯпyЃН
ЃЌЕБжБЯпyЃН![]() x+bгыЁбOЯрЧаЪБЃЌЩшЧаЕуЮЊEЃЌНЛyжсгкFЃЌЧѓГіЕуEЕФзјБъЃЌМДПЩХаЖЯЃЎ
x+bгыЁбOЯрЧаЪБЃЌЩшЧаЕуЮЊEЃЌНЛyжсгкFЃЌЧѓГіЕуEЕФзјБъЃЌМДПЩХаЖЯЃЎ
НтЃКЃЈ1ЃЉЂйШчЭМ1Љ1жаЃЌ
гЩЬтвтЃЌЕуOЃЌЕуAЪЧжБЯпyЃНЉx+2ЕФЁАПЩДяЕуЁБЃЌЕуBВЛЪЧжБЯпyЃНЉx+2ЕФЁАПЩДяЕуЁАЃЌ
ЙЪД№АИЮЊBЃЎ
ЂкШчЭМ1Љ2жаЃЌЕуAЪЧжБЯпyЃНЉx+3ЕФЁАПЩДяЕуЁБЧвЕуAВЛдкжБЯпlЩЯЃЈД№АИВЛЮЈвЛЃЌжБЯпдкЕуAЕФЩЯЗНМДПЩЃЉЃЎ

ЙЪД№АИЮЊyЃНЉx+3ЃЎ
ЂлШчЭМ1Љ3жаЃЌ

ЕБжБЯпyЃНkx+2ОЙ§ЕуBЪБЃЌkЃНЉ![]() ЃЌ
ЃЌ
ЕБжБЯпyЃНkx+2ОЙ§ЕуAЪБЃЌkЃНЉ1ЃЌ
ЙлВьЭМЯѓПЩжЊЃКЕБЕуAЁЂBжагаЧвНігавЛЕуЪЧжБЯпyЃНkx+2ЕФЁАПЩДяЕуЁБЃЌkЕФШЁжЕЗЖЮЇЪЧЉ1ЁмkЃМЉ![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЉ1ЁмkЃМЉ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЂйШчЭМ2Љ1жаЃЌ

Й§ЕуЃЈ0ЃЌ1ЃЉКЭЕуЃЈ0ЃЌЉ1ЃЉзїxжсЕФЦНааЯпЗжБ№НЛжБЯпyЃНЉ![]() xЉ2гкN1ЃЈЉ3
xЉ2гкN1ЃЈЉ3![]() ЃЌ1ЃЉЃЌN2ЃЈЉ
ЃЌ1ЃЉЃЌN2ЃЈЉ![]() ЃЌЉ1ЃЉЃЌ
ЃЌЉ1ЃЉЃЌ
Й§ЕуЃЈ1ЃЌ0ЃЉКЭЕуЃЈЉ1ЃЌ0ЃЉзїyжсЕФЦНааЯпЗжБ№НЛжБЯпyЃНЉ![]() xЉ2гкN3ЃЈ1ЃЌЉ
xЉ2гкN3ЃЈ1ЃЌЉ![]() Љ2ЃЉЃЌN4ЃЈЉ1ЃЌ
Љ2ЃЉЃЌN4ЃЈЉ1ЃЌ![]() Љ2ЃЉЃЌ
Љ2ЃЉЃЌ
ЙлВьЭМЯѓПЩжЊЃКNЪЧЁбOЕФЁАПЩДяЕуЁБЃЌxNЕФШЁжЕЗЖЮЇЉ3![]() ЁмxNЁмЉ
ЁмxNЁмЉ![]() ЛђЉ1ЁмxNЁм1ЃЎ
ЛђЉ1ЁмxNЁм1ЃЎ
ЙЪД№АИЮЊЉ3![]() ЁмxNЁмЉ
ЁмxNЁмЉ![]() ЛђЉ1ЁмxNЁм1ЃЎ
ЛђЉ1ЁмxNЁм1ЃЎ
ЂкШчЭМ2Љ2жаЃЌ

ЂйЕБN2гыN3жиКЯЃЌзјБъЮЊЃЈЉ1ЃЌЉ1ЃЉЪБЃЌЉ1ЃН![]() +bЃЌ
+bЃЌ
ЁрbЃНЉ1Љ![]() ЃЌ
ЃЌ
ЂкЕБжБЯпyЃН![]() x+bгыЁбOЯрЧаЪБЃЌЩшЧаЕуЮЊEЃЌНЛyжсгкFЃЎ
x+bгыЁбOЯрЧаЪБЃЌЩшЧаЕуЮЊEЃЌНЛyжсгкFЃЎ
гЩЬтвтдкRtЁїOEFжаЃЌЁЯOEFЃН90ЁуЃЌOEЃН1ЃЌЁЯEOFЃН30ЁуЃЌ
OFЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЙлВьЭМЯѓПЩжЊТњзуЬѕМўЕФbЕФжЕЮЊЉ1Љ![]() ЁмbЃМ
ЁмbЃМ![]() ЃЎ
ЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕу![]() дкХзЮяЯп
дкХзЮяЯп![]() ЩЯЃЌЧвХзЮяЯпгы
ЩЯЃЌЧвХзЮяЯпгы![]() жсЗжБ№НЛгкЕу
жсЗжБ№НЛгкЕу![]() КЭЕу
КЭЕу![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]()
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪН.
ЃЈ2ЃЉШєЕу![]() ЮЊХзЮяЯпЖдГЦжсЩЯЕФвЛИіЖЏЕуЃЌЧѓ
ЮЊХзЮяЯпЖдГЦжсЩЯЕФвЛИіЖЏЕуЃЌЧѓ![]() ЕФзюаЁжЕ.
ЕФзюаЁжЕ.
ЃЈ3ЃЉЕу![]() ЮЊХзЮяЯпЩЯГ§Еу
ЮЊХзЮяЯпЩЯГ§Еу![]() ЭтЕФвЛЕуЃЌШє
ЭтЕФвЛЕуЃЌШє![]() гы
гы![]() ЕФУцЛ§ЯрЕШЃЌЧѓЕу
ЕФУцЛ§ЯрЕШЃЌЧѓЕу![]() ЕФзјБъЁЃ
ЕФзјБъЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
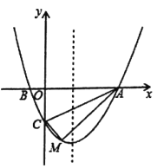
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНax2+bx+cжаЃЌКЏЪ§yгыздБфСПxЕФВПЗжЖдгІжЕШчБэЃК
x | Ё | Љ2 | Љ1 | 0 | 1 | 2 | 3 | Ё |
y | Ё | Љ8 | Љ3 | 0 | 1 | 0 | Љ3 | Ё |
ШєAЃЈmЃЌy1ЃЉЃЌBЃЈmЉ1ЃЌy2ЃЉСНЕуЖМдкИУКЏЪ§ЕФЭМЯѓЩЯЃЌЕБmТњзуЗЖЮЇ_____ЪБЃЌy1ЃМy2ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъзМБИНјвЛХњМОНкадаЁМвЕчЃЌУПИіНјМлЮЊ40дЊЃЌОЪаГЁдЄВтЃЌЯњЪлЖЈМлЮЊ50дЊЃЌПЩЪлГі400ИіЃЛЖЈМлУПдіМг1дЊЃЌЯњЪлСПНЋМѕЩй10ИіЃЌЩшУПИіЖЈМлдіМг![]() дЊ.
дЊ.
ЃЈ1ЃЉаДГіЪлГівЛИіПЩЛёЕУЕФРћШѓЪЧЖрЩйдЊЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉЃП
ЕФДњЪ§ЪНБэЪОЃЉЃП
ЃЈ2ЃЉЩЬЕъШєзМБИЛёЕУРћШѓ6000дЊЃЌВЂЧвЪЙНјЛѕСПНЯЩйЃЌдђУПИіЖЈМлЮЊЖрЩйдЊЃПгІНјЛѕЖрЩйИіЃП
ЃЈ3ЃЉгУКЌ![]() ЕФДњЪ§ЪНБэЪОЩЬЕъЛёЕУЕФРћШѓ
ЕФДњЪ§ЪНБэЪОЩЬЕъЛёЕУЕФРћШѓ![]() дЊЃЌВЂМЦЫуЩЬЕъШєвЊЛёЕУзюДѓРћШѓЃЌдђУПИігІЖЈМлЖрЩйдЊЃПЛёЕУЕФзюДѓРћШѓЪЧЖрЩйдЊЃП
дЊЃЌВЂМЦЫуЩЬЕъШєвЊЛёЕУзюДѓРћШѓЃЌдђУПИігІЖЈМлЖрЩйдЊЃПЛёЕУЕФзюДѓРћШѓЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
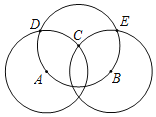
ЁОЬтФПЁПвбжЊЕуAЁЂBЃЈABЃМ2ЃЉЃЌЯжУЛгажБГпЃЌжЛгавЛАбЩњатЕФдВЙцЃЌНіФмзіГіАыОЖЮЊ1ЕФдВЃЌФмЗёдкЦНУцФкевЕНвЛЕуFЃЌЪЙЕУЁїABFЪЧЕШБпШ§НЧаЮЃП
аЁЬьОЙ§ЬНОПЭъГЩСЫвдЯТЕФзїЭМВНжшЃК
ЕквЛВНЃКЗжБ№вдЕуAЁЂBЮЊдВаФЃЌ1ЮЊАыОЖзїдВЃЌСНдВНЛгкЕуCЃЛ
ЕкЖўВНЃКвдCЮЊдВаФЃЌ1ЮЊАыОЖзїдВНЛЕквЛВНжаЕФСНдВгкЕуDЁЂEЃЛ
ЕкШ§ВНЃКЗжБ№вдDЁЂEЮЊдВаФЃЌ1ЮЊАыОЖзїдВЃЌСНдВНЛгкЕуCЁЂFЃЌ
ЃЈ1ЃЉЧыНЋЭМВЙГфЭъећЃЌВЂзїГіЁїABFЃЎ
ЃЈ2ЃЉвдЯТЫЕЗЈжаЃЌ
ЂйЕуCдкЯпЖЮABЕФДЙжБЦНЗжЯпЩЯЃЛ
ЂкЁїCADКЭЁїCBEЖМЪЧЕШБпШ§НЧаЮЃЛ
ЂлЕуCдкЯпЖЮAFЕФДЙжБЦНЗжЯпЩЯЃЛ
ЂмЁїABFЪЧЕШБпШ§НЧаЮЃЌ
е§ШЗЕФгаЁЁ ЁЁЃЎЃЈЬюЩЯЫљгае§ШЗЕФађКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌХзЮяЯп![]() ЕФЖЅЕуЮЊ
ЕФЖЅЕуЮЊ![]() ЃЌгы
ЃЌгы![]() жсНЛгк
жсНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌЧв
СНЕуЃЌЧв![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЎ
ЃЎ
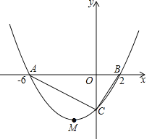
![]() ЧѓХзЮяЯпЕФКЏЪ§НтЮіЪНЃЛ
ЧѓХзЮяЯпЕФКЏЪ§НтЮіЪНЃЛ
![]() Чѓ
Чѓ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
![]() ФмЗёдкХзЮяЯпЕкШ§ЯѓЯоЕФЭМЯѓЩЯевЕНвЛЕу
ФмЗёдкХзЮяЯпЕкШ§ЯѓЯоЕФЭМЯѓЩЯевЕНвЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЕФУцЛ§зюДѓЃПШєФмЃЌЧыЧѓГіЕу
ЕФУцЛ§зюДѓЃПШєФмЃЌЧыЧѓГіЕу![]() ЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() КЭжБЯпlЃК
КЭжБЯпlЃК![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃКХзЮяЯпгыжБЯпвЛЖЈгаСНИіВЛЭЌЕФНЛЕуЃЛ
ЃЈ2ЃЉЩшAЁЂBЪЧХзЮяЯпгыжБЯпЕФСНИіНЛЕуЃЌЕуPЪЧЯпЖЮABЕФжаЕуЃЌвбжЊЮоТлaЮЊКЮжЕЃЌЕуPдквЛЬѕЖЈХзЮяЯпЩЯЃЌЪдЧѓетЬѕЖЈХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ3ЃЉЩшAЁЂBЪЧХзЮяЯпгыжБЯпЕФСНИіНЛЕуЃЌНЋжБЯпlЯђЯТЦНвЦ7ИіЕЅЮЛЧЁКУгыХзЮяЯпгаЧвжЛгавЛИіЙЋЙВЕуCЃЌЧѓЁїABCЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯCЃН90ЁуЃЌЕуDдкABЩЯЃЌвдADЮЊжБОЖЕФЁбOгыBCЯрНЛгкЕуEЃЌгыACЯрНЛгкЕуFЃЌAEЦНЗжЁЯBACЃЎ
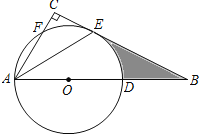
ЃЈ1ЃЉЧѓжЄЃКBCЪЧЁбOЕФЧаЯпЃЎ
ЃЈ2ЃЉШєЁЯEABЃН30ЁуЃЌODЃН3ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ЃЈ3ЃЉШєADЃН5ЃЌAEЃН4ЃЌЧѓAFЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
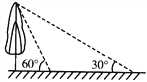
ЁОЬтФПЁПШчЭМЃЌаЃдАФкгавЛПУгыЕиУцДЙжБЕФЪїЃЌЪ§бЇаЫШЄаЁзщСНДЮВтСПЫќдкЕиУцЩЯЕФгАзгЃЌЕквЛДЮЪЧбєЙтгыЕиУцГЩ60ЁуНЧЪБЃЌЕкЖўДЮЪЧбєЙтгыЕиУцГЩ30ЁуНЧЪБЃЌСНДЮВтСПЕФгАГЄЯрВю8УзЃЌдђЪїИп_____________Уз(НсЙћБЃСєИљКХ)ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com