
【题目】某商店准备进一批季节性小家电,每个进价为40元,经市场预测,销售定价为50元,可售出400个;定价每增加1元,销售量将减少10个,设每个定价增加![]() 元.
元.
(1)写出售出一个可获得的利润是多少元(用含![]() 的代数式表示)?
的代数式表示)?
(2)商店若准备获得利润6000元,并且使进货量较少,则每个定价为多少元?应进货多少个?
(3)用含![]() 的代数式表示商店获得的利润
的代数式表示商店获得的利润![]() 元,并计算商店若要获得最大利润,则每个应定价多少元?获得的最大利润是多少元?
元,并计算商店若要获得最大利润,则每个应定价多少元?获得的最大利润是多少元?
【答案】(1)![]() 元 ;(2)定价为70元,进货200个;(3)每个定价65元时,利润最大为6250元.
元 ;(2)定价为70元,进货200个;(3)每个定价65元时,利润最大为6250元.
【解析】
(1)根据利润=售价进价,列关系式即可;
(2)首先求出销售量为40010x,然后根据总利润=每个的利润×销售量,列方程求解,根据题意取舍即可;
(3)列出利润![]() 的函数关系式,利用二次函数的性质求最值即可.
的函数关系式,利用二次函数的性质求最值即可.
解:(1)售出一个可获得的利润是![]() (元);
(元);
(2)由于定价每增加1元,销售量将减少10个,故销售量为(40010x)个,
由题意得:![]() ,
,
解得:![]() ,
,![]() ,
,
∵要使进货量较少,
∴![]() ,
,
∴定价为50+20=70元/个,进货![]() 个;
个;
(3)由题意得:![]()
![]() ,
,
当![]() 时,
时,![]() (元),
(元),
∵![]() (元),
(元),
∴每个定价65元时,利润最大为6250元.


科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2.
(1)求实数k的取值范围.
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() 是
是![]() 的角平分线,
的角平分线,![]() 是
是![]() 上一点,以点
上一点,以点![]() 为圆心,
为圆心,![]() 的长为半径作
的长为半径作![]() 与
与![]() 相切于点
相切于点![]() .
.
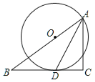
(1)求证:![]() =
=![]()
(2)若________=![]() ,________=
,________=![]() ,填空
,填空
①![]() ________的半径长为________;
________的半径长为________;
②![]() ________=________.
________=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行摸牌游戏.现有十张形状大小完全相同的牌,正面分别标有数字1~10.从中选出一些牌,将这些牌背面朝上,洗匀后放在桌子上.甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.若两人抽取的数字和为2的倍数,则甲获胜;其余情况,乙获胜.
(1)若选出三张分别标有数字2、3、5的牌,这个游戏公平吗?请利用树状图或列表法来解释说明.
(2)乙说:“若我在2、3、5三张牌外再选一张牌,共四张牌进行游戏,则我可以让自己获胜的可能性比甲大”,请判断乙的说法是否正确,若正确,请写出乙可以再选哪些牌让自己获胜的可能性比甲大;若不正确,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于给定的图形G和点P,若点P可通过一次向上或向右平移n(n>0)个单位至图形G上某点P′,则称点P为图形G的“可达点”,特别地,当点P在图形G上时,点P为图形G的“可达点”.
(1)如图1,在平面直角坐标系xOy中,点A(1,1),B(2,1),
①在点O、A、B中,不是直线y=﹣x+2的“可达点”的是 ;
②若点A是直线l的“可达点”且点A不在直线l上,写出一条满足要求的直线l的表达式: ;
③若点A、B中有且仅有一点是直线y=kx+2的“可达点”,则k的取值范围是 .
(2)如图2,在平面直角坐标系xOy中,⊙O的半径为1,直线l:y=﹣![]() x+b.
x+b.
①当b=﹣2时,若直线m上一点N(xN,yN)满足N是⊙O的“可达点”,直接写出xN的取值范围 ;
②若直线m上所有的⊙O的“可达点”构成一条长度不为0的线段,直接写出b的取值范围 .
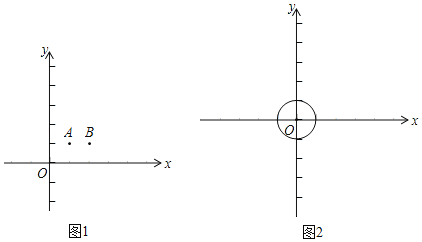
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在歌唱比赛中,一位歌手分别转动如下的两个转盘(每个转盘都被分成3等份)一次,根据指针指向的歌曲名演唱两首曲目.

(1)转动转盘①时,该转盘指针指向歌曲“3”的概率是 ;
(2)若允许该歌手替换他最不擅长的歌曲“3”,即指针指向歌曲“3”时,该歌手就选择自己最擅长的歌曲“1”, 请用树形图或列表法中的一种,求他演唱歌曲“1”和“4”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com