
【题目】如图,![]() 中,
中,![]() 是
是![]() 的角平分线,
的角平分线,![]() 是
是![]() 上一点,以点
上一点,以点![]() 为圆心,
为圆心,![]() 的长为半径作
的长为半径作![]() 与
与![]() 相切于点
相切于点![]() .
.
(1)求证:![]() =
=![]()
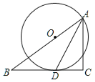
(2)若________=![]() ,________=
,________=![]() ,填空
,填空
①![]() ________的半径长为________;
________的半径长为________;
②![]() ________=________.
________=________.
【答案】(1)见解析;(2)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)连接OD,如图,先证明OD∥AC,再根据切线的性质得到OD⊥BC,则AC⊥BC,从而可判断∠ACB=90°;
(2)根据题意,若AC=3,BC=4,①先利用勾股定理计算出AB=5,设⊙O的半径为r,则OA=OD=r,OB=5-r,证明△BDO∽△BCA,利用相似比得到![]() ,然后解关于r的方程即可;
,然后解关于r的方程即可;
②利用△BDO∽△BCA得到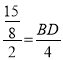 ,则可计算出BD=
,则可计算出BD=![]() ,从而得到CD=
,从而得到CD=![]() ,然后根据正切的定义计算tan∠CAD的值.
,然后根据正切的定义计算tan∠CAD的值.
证明:(1)连接![]() ,如图,
,如图,
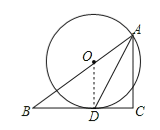
∵![]() 是
是![]() 的角平分线,
的角平分线,
∴![]() =
=![]() ,
,
∵![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() ,
,
∵![]() 与
与![]() 相切于点
相切于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() =
=![]() ;
;
(2)①在Rt△ABC中,AB=![]() ,
,
设⊙O的半径为r,则OA=OD=r,OB=5-r,
∵OD∥AC,
∴△BDO∽△BCA,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
即⊙O的半径为:![]() ;
;
②∵△BDO∽△BCA,
∴![]() ,即
,即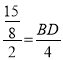 ,
,
解得:BD=![]() ,
,
∴CD=![]() ,
,
在Rt△ACD中,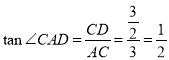 ;
;
故答案为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】材料一:把一个自然数的个位数字截太再用余下的数加上个位数的4倍,如果和是13的倍数,则原数能被13整除.如果和太大不易看出是否13的倍数,可重复上述「截尾、倍大、相加、验和」的过程,直到能清楚判断为止.例如,判断377是否13的倍数的过程如下:37+7×4=65,65÷13=5,所以,377是13的倍数;又例如判断8632是否13的倍数的过程如下:863+2×4=871,87+1×4=91,91÷13=7.所以,8632是13的倍数.
材料二:若一个四位自然数n,满足千位与个位相同,百位与十位相同,我们称这个数为“对称数”.将“对称数”n的前两位与后两位交换位置得到一个新的n′,记F(n)=![]() ,例如n=3113,n′=1331,(3113)=
,例如n=3113,n′=1331,(3113)=![]() =18.
=18.
(1)请用材料一的方法判断1326与3366能否被13整除;
(2)若m、p是“对称数”,其中m=![]() ,p=
,p=![]() (0≤b<a≤5,1≤c<a≤5且a,b,c均为整数),若m能被l3整除,且F(m)﹣F(p)=36,求p.
(0≤b<a≤5,1≤c<a≤5且a,b,c均为整数),若m能被l3整除,且F(m)﹣F(p)=36,求p.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5条.设每条裤子的售价为![]() 元(
元(![]() 为正整数),每月的销售量为
为正整数),每月的销售量为![]() 条.
条.
(1)直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)设该网店每月获得的利润为![]() 元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2(m﹣1)x+m2﹣3=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若m为非负整数,且该方程的根都是无理数,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣8 | ﹣3 | 0 | 1 | 0 | ﹣3 | … |
若A(m,y1),B(m﹣1,y2)两点都在该函数的图象上,当m满足范围_____时,y1<y2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备进一批季节性小家电,每个进价为40元,经市场预测,销售定价为50元,可售出400个;定价每增加1元,销售量将减少10个,设每个定价增加![]() 元.
元.
(1)写出售出一个可获得的利润是多少元(用含![]() 的代数式表示)?
的代数式表示)?
(2)商店若准备获得利润6000元,并且使进货量较少,则每个定价为多少元?应进货多少个?
(3)用含![]() 的代数式表示商店获得的利润
的代数式表示商店获得的利润![]() 元,并计算商店若要获得最大利润,则每个应定价多少元?获得的最大利润是多少元?
元,并计算商店若要获得最大利润,则每个应定价多少元?获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
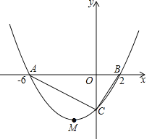
【题目】如图所示,抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点,且
两点,且![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
![]() 求抛物线的函数解析式;
求抛物线的函数解析式;
![]() 求
求![]() 的面积;
的面积;
![]() 能否在抛物线第三象限的图象上找到一点
能否在抛物线第三象限的图象上找到一点![]() ,使
,使![]() 的面积最大?若能,请求出点
的面积最大?若能,请求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶.已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需_________分钟到达终点B.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com