
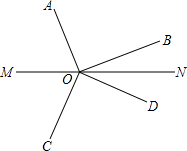
 点O在直线MN上,∠AOB=∠COD=90°.
点O在直线MN上,∠AOB=∠COD=90°.分析 (1)首先根据题意,分别求出∠BOD、∠AOC的度数,然后根据OM平分∠AOC,求出∠AOM的度数,即可求出∠BON的度数是多少.
(2)根据题意,分两种情况:①当OP在OC、OD之间时;②当OP在OB、OD之间时;然后根据∠BOP:∠DOP=3:2,分类讨论,求出∠PON与∠BOD的数量关系即可.
解答 解:(1)如图1,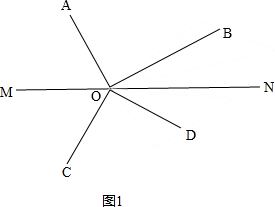 ,
,
∵∠BOC=150°,∠COD=90°,
∴∠BOD=150°-90°=60°,
∴∠AOC=360-90°-60°-90°=120°,
∵OM平分∠AOC,
∴∠AOM=120°÷2=60°,
∴∠BON=180°-60°-90°=30°.
(2)①如图2,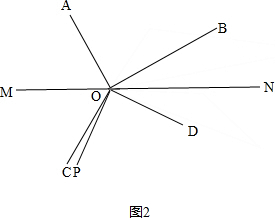 ,
,
设∠AOM=x,
∵2∠AOM-∠MOC=90°,
∴∠MOC=2x-90°,
∴∠BOD=360°-90°-90°-(2x-90°+x)=270°-3x,
∴∠DON=180°-90°-(2x-90°)=180°-2x,
∵∠BOP:∠DOP=3:2,
∴∠BOD:∠DOP=1:2,
∴∠DOP=2∠BOD=2(270°-3x)=540°-6x,
∴∠PON=∠DOP+∠DON=(540°-6x)+(180°-2x)=720°-8x,
∵720°-8x=$\frac{8}{3}$(270°-3x),
∴∠PON=$\frac{8}{3}$∠BOD.
②如图3,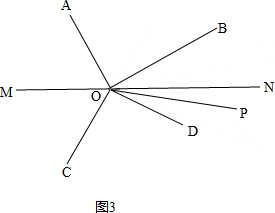 ,
,
设∠AOM=x,
∵2∠AOM-∠MOC=90°,
∴∠MOC=2x-90°,
∴∠BOD=360°-90°-90°-(2x-90°+x)=270°-3x,
∴∠DON=180°-90°-(2x-90°)=180°-2x,
∵∠BOP:∠DOP=3:2,
∴∠DOP=∠BOD×$\frac{2}{2+3}$=(270°-3x)×$\frac{2}{5}$=108°-1.2x,
∴∠PON=∠DON-∠DOP=(180°-2x)-(108°-1.2x)=72°-0.8x,
∵72°-0.8x=$\frac{4}{15}$(270°-3x),
∴∠PON=$\frac{4}{15}$∠BOD.
综上,可得
∠PON=$\frac{4}{15}$∠BOD或∠PON=$\frac{8}{3}$∠BOD.
点评 (1)此题主要考查了角的计算,要熟练掌握,解答此题的关键是弄清楚各个角之间的关系.
(2)此题还考查了角平分线的性质和应用,要熟练掌握,解答此题的关键是要明确:一个角的平分线把这个角分成两个大小相同的角.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向左平移1个单位,向上平移3个单位 | |
| B. | 向右平移1个单位,向上平移3个单位 | |
| C. | 向左平移1个单位,向下平移3个单位 | |
| D. | 向右平移1个单位,向下平移3个单位 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠A=∠D | B. | ∠C=∠F | C. | ∠B=∠E | D. | ∠C=∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com