
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是直线
是直线![]() 上一点.
上一点.
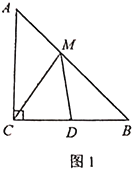
(1)如图1,若![]() ,点
,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 是线段
是线段![]() 上一动点,求
上一动点,求![]() 周长的最小值.
周长的最小值.
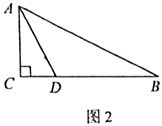
(2)如图2,若![]() ,
,![]() ,是否存在点
,是否存在点![]() ,使以
,使以![]() ,
,![]() ,
,![]() 为顶点的三角形是等腰三角形,若存在,请直按写出线段
为顶点的三角形是等腰三角形,若存在,请直按写出线段![]() 的长度:若不存在,请说明理由.
的长度:若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,CD=3或8或
;(2)存在,CD=3或8或![]() 或
或![]() .
.
【解析】
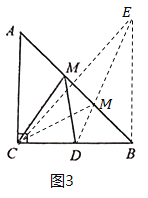
(1)本小题是典型的“将军饮马”问题,只要作点C关于直线AB的对称点E,连接BE、DE,DE交AB于点M,如图3,则此时![]() 的周长最小,且最小值就是CD+DE的长,由于CD易求,故只要计算DE的长即可,由轴对称的性质和等腰直角三角形的性质可得BE=BC=2,∠DBE=90°,然后根据勾股定理即可求出DE,问题即得解决;
的周长最小,且最小值就是CD+DE的长,由于CD易求,故只要计算DE的长即可,由轴对称的性质和等腰直角三角形的性质可得BE=BC=2,∠DBE=90°,然后根据勾股定理即可求出DE,问题即得解决;
(2)由于点![]() 是直线
是直线![]() 上一点,所以需分三种情况讨论:①当AB=AD时,如图4,根据等腰三角形的性质求解即可;②当BD=BA时,如图5,根据勾股定理和等腰三角形的定义求解;③当DA=DB时,如图6,设CD=x,然后在直角△ACD中根据勾股定理求解即可.
上一点,所以需分三种情况讨论:①当AB=AD时,如图4,根据等腰三角形的性质求解即可;②当BD=BA时,如图5,根据勾股定理和等腰三角形的定义求解;③当DA=DB时,如图6,设CD=x,然后在直角△ACD中根据勾股定理求解即可.
解:(1)作点C关于直线AB的对称点E,连接BE、DE,DE交AB于点M,连接CM,如图3,则此时![]() 的周长最小.
的周长最小.
∵![]() ,
,![]() ,点
,点![]() 是
是![]() 边的中点,∴∠CBA=45°,BD=CD=1,
边的中点,∴∠CBA=45°,BD=CD=1,
∵点C、E关于直线AB对称,∴BE=BC=2,∠EBA=∠CBA=45°,∴∠DBE=90°,
∴![]() .
.
∴![]() 的周长的最小值=CD+DE=
的周长的最小值=CD+DE=![]() ;
;
(2)由于点![]() 是直线
是直线![]() 上一点,所以需分三种情况讨论:
上一点,所以需分三种情况讨论:
①当AB=AD时,如图4,此时CD=CB=8;
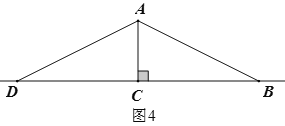
②当BD=BA时,如图5,在直线BC上存在两点符合题意,即D1、D2,
∵![]() ,∴
,∴![]() ,
,![]() ;
;

③当DA=DB时,如图6,此时点D为线段AB的垂直平分线与直线BC的交点,设CD=x,则BD=AD=8-x,在直角△ACD中,根据勾股定理,得:![]() ,解得:x=3,即CD=3.
,解得:x=3,即CD=3.

综上,在直线BC上存在点![]() ,使以
,使以![]() ,
,![]() ,
,![]() 为顶点的三角形是等腰三角形,且CD=3或8或
为顶点的三角形是等腰三角形,且CD=3或8或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】某工厂的厂门形状如图(厂门上方为半圆形拱门),现有四辆装满货物的卡车,外形宽都是2.0米,高分别为2.8米,3.1米,3.4米,3.7米,则能通过该工厂厂门的车辆数是( )(参考数据:![]() ,
,![]() ,
,![]() )
)
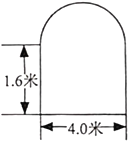
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]() 的小正方形,五块是长为
的小正方形,五块是长为![]() ,宽为
,宽为![]() 的全等小矩形,且
的全等小矩形,且![]() .
.
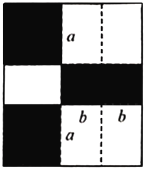
(1)观察图形,将多项式![]() 分解因式;
分解因式;
(2)若每块小矩形的面积为10,四个正方形的面积和为58.求下列代数式的值:
①![]() .
.
②![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,D,E 分别是 AB,BC 上的点,且 DE∥AC,若 S△BDE:S△CDE=1:3,则S△DEB: S△ADC=( )

A. 1:5 B. 1:9 C. 1:10 D. 1:12
查看答案和解析>>
科目:初中数学 来源: 题型:
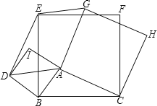
【题目】以![]() 的各边,在边
的各边,在边![]() 的同侧分别作三个正方形.他们分别是正方形
的同侧分别作三个正方形.他们分别是正方形![]() ,
,![]() ,
,![]() ,试探究:
,试探究:
![]() 如图中四边形
如图中四边形![]() 是什么四边形?并说明理由.
是什么四边形?并说明理由.
![]() 当
当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是矩形?
是矩形?
![]() 当
当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形?
是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表。
组别 | 分数段 | 频次 | 频率 |
A | 60x<70 | 17 | 0.17 |
B | 70x<80 | 30 | a |
C | 80x<90 | b | 0.45 |
D | 90x<100 | 8 | 0.08 |
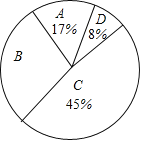
请根据所给信息,解答以下问题:
(1)表中a=___,b=___;
(2)请计算扇形统计图中B组对应扇形的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的![]() 月
月![]() 日为世界环保日,为了提倡低碳环保,某公司决定购买
日为世界环保日,为了提倡低碳环保,某公司决定购买![]() 台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买
台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备多花
台乙型设备多花![]() 万元,购买
万元,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备少花
台乙型设备少花![]() 万元.
万元.
(1)求甲、乙两种型号设备每台的价格;
(2)该公司经决定购买甲型设备不少于![]() 台,预算购买节省能源的新设备资金不超过
台,预算购买节省能源的新设备资金不超过![]() 万元,你认为该公司有哪几种购买方案;
万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备每月的产量为![]() 吨,乙型设备每月的产量为
吨,乙型设备每月的产量为![]() 吨.若每月要求产量不低于
吨.若每月要求产量不低于![]() 吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com