练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某工厂的厂门形状如图(厂门上方为半圆形拱门)，现有四辆装满货物的卡车，外形宽都是2.0米，高分别为2.8米，3.1米，3.4米，3.7米，则能通过该工厂厂门的车辆数是( )(参考数据：，，)

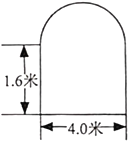
    A.1B.2C.3D.4

    【答案】B

    【解析】

    如图，在直角△COD中，根据勾股定理求出CD的长，进而可得CB的长，然后与四辆车的车高进行比较即得答案．

    解：∵车宽是2米，∴卡车能否通过，只要比较距厂门中线1米处高度与车高即可．

    如图，在直角△COD中，∵OC=2，OD=1，∴米，∴CB=CD+BD=1.73+1.6=3.33米．

    ∵2.8<3.33，3.1<3.33，3.4>3.33，3.7>3.33，∴这四辆车中车高为2.8米和3.1米的能够通过，而车高为3.4米和3.7米的则不能通过．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】现有3张边长为的正方形纸片（类），5张边长为的矩形纸片（类），5张边长为的正方形纸片（类）．

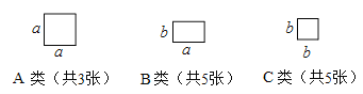
    我们知道：多项式乘法的结果可以利用图形的面积表示．

    例如：就能用图①或图②的面积表示．

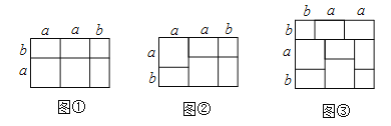
    （1）请你写出图③所表示的一个等式：_______________；

    （2）如果要拼一个长为，宽为的长方形，则需要类纸片_____张，需要类纸片_____张，需要类纸片_____张；

    （3）从这13张纸片中取出若干张，每类纸片至少取出一张，把取出的这些纸片拼成一个正方形（按原纸张进行无缝隙，无重叠拼接），则拼成的正方形的边长最长可以是_______（用含的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场服装部为了调动营业员的积极性，决定实行目标管理，根据目标完成的情况对营业员进行适当的奖励．为了确定一个适当的月销售目标，商场服装部统计了每位营业员在某月的销售额（单位：万元），数据如下：

    17

    18

    16

    13

    24

    15

    28

    26

    18

    19

    22

    17

    16

    19

    32

    30

    16

    14

    15

    26

    15

    32

    23

    17

    15

    15

    28

    28

    16

    19

    对这30个数据按组距3进行分组，并整理、描述和分析如下．

    频数分布表

    组别

    一

    二

    三

    四

    五

    六

    七

    销售额

    频数

    7

    9

    3

    2

    2

    数据分析表

    平均数

    众数

    中位数

    20.3

    18

    请根据以上信息解答下列问题：

    （1）填空：a=　　，b=　　，c=　　；

    （2）若将月销售额不低于25万元确定为销售目标，则有　　位营业员获得奖励；

    （3）若想让一半左右的营业员都能达到销售目标，你认为月销售额定为多少合适？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明和他的同学根据抛掷两枚硬币时记录的实验结果，制作“出现两个正面”的频数、频率表如下：

    抛掷次数

    出现两个正面的频数

    出现两个正面的频率

    在大数次抛掷两枚硬币的实验中，出现两个正面的频率稳定在________附近；

    小明和表弟玩一个抛掷两枚硬币的游戏，小明制定的游戏规则如下：抛出两个正面–小明的表弟赢分；抛出其他结果–小明赢分；谁先到分，谁就得胜．你认为这个游戏规则公平吗？说说理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标中，边长为2的正方形的两顶点、分别在轴、轴的正半轴上，点在原点.现将正方形绕点顺时针旋转，当点第一次落在直线上时停止旋转，旋转过程中，边交直线于点，边交轴于点

    （1）求边在旋转过程中所扫过的面积；

    （2）旋转过程中，当和平行时，求正方形旋转的度数；

    （3）设的周长为，在旋转正方形的过程中，值是否有变化？请证明你的结论.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】第7届世界军人运动会于2019年10月18日在武汉开幕，为备战本届军运会，某运动员进行了多次打靶训练，现随机抽取该运动员部分打靶成绩进行整理分析，共分成四组：(优秀)、(良好)、(合格)、(不合格)，绘制了如下不完整的统计图：

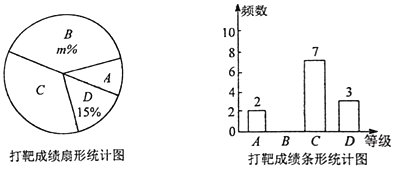
    根据以上信息，解答下列问题：

    (1)直接写出本次统计成绩的总次数和图中的值.

    (2)求扇形统计图中(合格)所对应圆心角的度数.

    (3)请补全条形统计图.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，点是直线上一点.

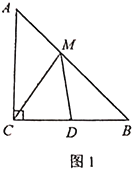
    (1)如图1，若，点是边的中点，点是线段上一动点，求周长的最小值.

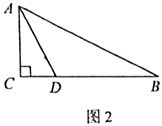
    (2)如图2，若，，是否存在点，使以，，为顶点的三角形是等腰三角形，若存在，请直按写出线段的长度：若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2+bx+c的图象与x轴交于点（﹣2，0）、（x1，0），且1＜x1＜2，与y轴正半轴的交点在（0，2）的下方，在原点的上方．下列结论：①4a﹣2b+c=0；②2a﹣b＜0；③2a﹣b＞﹣1；④2a+c＜0；⑤b＞a；其中正确结论的个数是（　　）

    A. 2 B. 3 C. 4 D. 5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知某服装厂现有种布料70米，种布料52米，现计划用这两种布料生产、两种型号的时装共80套.已知做一套型号的时装需用A种布料1.1米，种布料0.4米，可获利50元；做一套型号的时装需用种布料0.6米，种布料0.9米，可获利45元.设生产型号的时装套数为，用这批布料生产两种型号的时装所获得的总利润为元.

    （1）求（元）与（套）的函数关系式.

    （2）有几种生产方案？

    （3）如何生产使该厂所获利润最大？最大利润是多？

    查看答案和解析>>

    同步练习册答案