
| A. | 在等式ax=bx两边除以x,可得a=b | B. | 由等式a2=b2,一定有a=b | ||
| C. | 在等式$\frac{a}{3}=\frac{b}{3}$两边除以3,得到a=b | D. | 由等式5x=4x+1,可得x=1 |
分析 根据等式的两边同时加上(或减去)同一个数(或字母),等式仍成立;等式的两边同时乘以(或除以)同一个不为0数(或字母),等式仍成立.
解答 解:A、当x=0时,等式ax=bx两边除以x无意义,故A错误;
B、等式a2=b2,一定有a=b或a=-b,故B错误;
C、等式$\frac{a}{3}=\frac{b}{3}$两边除以3,得到$\frac{a}{9}$=$\frac{b}{9}$,故C错误;
D、等式5x=4x+1,两边都减4x,得x=1,故D正确;
故选:D.
点评 本题主要考查了等式的基本性质,等式的两边同时加上(或减去)同一个数(或字母),等式仍成立;等式的两边同时乘以(或除以)同一个不为0数(或字母),等式仍成立.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 13(1-x)2=20 | B. | 20(1-x)2=13 | C. | 20(1+x)2=13 | D. | 13(1+x)2=20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
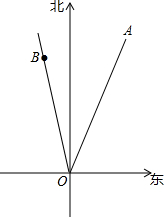 2014年第10号台风“麦德姆”,是2014年度对我国破坏性最大的一次台风,“麦德姆”台风从福建登陆后一路北上,在青岛荣成再次登陆.如图所示,某时,台风“麦德姆”的中心在点O沿北偏东20°的方向以30km/h的速度移动,在点O北偏西10°的方向距离O点360km处有一个小岛B.如果台风中心的最大风力为14级,每远离台风中心20千米风力减弱一级,小岛A的风力达到四级或四级以上,则称其受台风影响.
2014年第10号台风“麦德姆”,是2014年度对我国破坏性最大的一次台风,“麦德姆”台风从福建登陆后一路北上,在青岛荣成再次登陆.如图所示,某时,台风“麦德姆”的中心在点O沿北偏东20°的方向以30km/h的速度移动,在点O北偏西10°的方向距离O点360km处有一个小岛B.如果台风中心的最大风力为14级,每远离台风中心20千米风力减弱一级,小岛A的风力达到四级或四级以上,则称其受台风影响.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
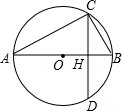 如图,AB为⊙O直径,弦CD⊥AB,垂足为H,已知⊙O的半径为2,CD=2$\sqrt{3}$.
如图,AB为⊙O直径,弦CD⊥AB,垂足为H,已知⊙O的半径为2,CD=2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com