
【题目】观察下列三行数
①﹣3,9,﹣27,81,﹣243,……
②﹣5,7,﹣29,79,﹣245,……
③﹣1,3,﹣9,27,﹣81,……
第①行数排列律是_____;第②行数与第①行数的关系是_____;第③行数与第①行数的关系是_____.
【答案】把一个数乘以﹣3得到它后面的一个数 第②行中的数比第①行中对应位置的数小2 第②行中的数是第①行中对应位置的数乘以![]()
【解析】
仔细观察三行数,寻找其中规律进行解答即可.
(1)﹣3×(﹣3)=9,9×(﹣3)=﹣27,﹣27×(﹣3)=81,81×(﹣3)=﹣243,因此第①行的排列律是把一个数乘以﹣3得到它后面的一个数;(2)﹣3-2=﹣5,9-2=7,﹣27-2=﹣29,81-2=79,-243-2=﹣245,因此第②行数与第①行数的关系是第②行中的数比第①行中对应位置的数小2;(3)-3×![]() =﹣1,9×
=﹣1,9×![]() =3,﹣27×
=3,﹣27×![]() =﹣9,81×
=﹣9,81×![]() ==27,-243×
==27,-243×![]() =﹣81,因此第③行数与第①行数的关系是第②行中的数是第①行中对应位置的数乘以
=﹣81,因此第③行数与第①行数的关系是第②行中的数是第①行中对应位置的数乘以![]() .
.


科目:初中数学 来源: 题型:
【题目】如图是某小区的一个健向器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,BC∥OA,∠B=∠A=100°,试回答下列问题:
(1)如图①,求证:OB∥AC. 
(2)如图②,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.则∠EOC的度数等于;(在横线上填上答案即可). 
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值. 
(4)在(3)的条件下,如果平行移动AC的过程中,若使∠OEB=∠OCA,求∠OCA度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,BC∥OA,∠B=∠A=100°,试回答下列问题:
(1)如图①,求证:OB∥AC. 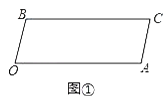
(2)如图②,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.求∠EOC的度数. 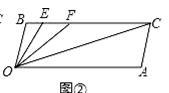
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值. 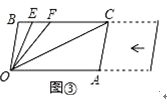
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l上依次有三点A、B、C,且AB=8、BC=16,点P为射线AB上一动点,将线段AP进行翻折得到线段PA′(点A落在直线l上点A′处、线段AP上的所有点与线段PA′上的点对应).
(1)若翻折后A′C=2,则翻折前线段AP= .
(2)若点P在线段BC上运动,点M为线段A′C的中点,直接写出线段PM的长度.
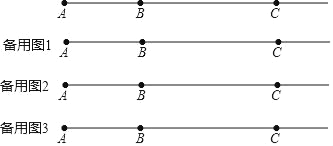
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A、B表示的数分别是有理数a,b.
(1)若点A在原点的左侧,点B在原点的右侧,且|a|=|b|,则a与b的关系是 ,用式子表示为 .
(2)若a=﹣5,b=1![]()
①分别写出a,b的相反数;
②求|a![]() |﹣|b
|﹣|b![]() |的值.
|的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中标明了小英家附近的一些地方,已知游乐场的坐标为(3,2).
(1)在图中建立平面直角坐标系,并写出汽车站和消防站的坐标;
(2)某星期日早晨,小英同学从家里出发,沿(3,2),(3,-1),(1,-1),(-1,-2),(-3,-1)的路线转了一下,又回到家里,写出路上她经过的地方.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两艘轮船同时从港口O出发,甲轮船以20海里/时的速度向南偏东45°方向航行,乙轮船向南偏西45°方向航行.已知它们离开港口O两小时后,两艘轮船相距50海里,求乙轮船平均每小时航行多少海里?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com