
【题目】二次函数![]() (a≠0)的图象如图所示,则下列命题中正确的是( )
(a≠0)的图象如图所示,则下列命题中正确的是( )
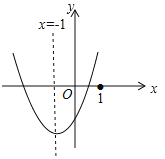
A. a >b>c
B. 一次函数y=ax +c的图象不经第四象限
C. m(am+b)+b<a(m是任意实数)
D. 3b+2c>0
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() ,点
,点![]() .
.
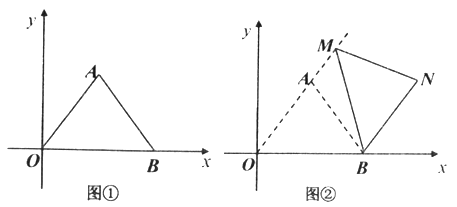
(Ⅰ)如图①,求AB的长;
(Ⅱ)如图②,把图①中的![]() 绕点B顺时针旋转,使点O的对应点AM恰好落在OA延长线上,N是点A旋转后的对应点.
绕点B顺时针旋转,使点O的对应点AM恰好落在OA延长线上,N是点A旋转后的对应点.
①求证:![]() ;②求点N的坐标;
;②求点N的坐标;
(Ⅲ)点C是OB的中点,点D为线段OA上的动点,在![]() 绕点B顺时针旋转过程中,点D的对应点是P,求线段CP长的取值范围(直接写出结果).
绕点B顺时针旋转过程中,点D的对应点是P,求线段CP长的取值范围(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)
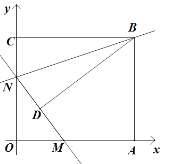
如图,矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上,线段OA、OC的长度满足方程|x-15|+=0(OB>OC),直线y=kx+b分别与x轴、y轴交于M、N两点,连接BN.将△BCN沿直线BN折叠,点C恰好落在直线MN上的点D处,且tan∠CBD=.
⑴ 求点B的坐标.
⑵ 求直线BN的解析式.
⑶ 将直线BN以每秒1个单位长度的速度沿y轴向下平移,求直线BN扫过矩形AOCB的面积S关于运动的时间t(0<t≤13)的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了了解初中学校“高效课堂”的有效程度,并就初中生在课堂上是否具有“主动质疑”、“独立思考”、“专注听讲”、“讲解题目”等学习行为进行评价.为此,该市教研部门开展了一次抽样调查, 并将调查结果绘制成尚不完整的条形统计图和扇形统计图( 如图所示),请根据图中信息解答下列问题:
(1)这次抽样调查的样本容量为 .
(2)在扇形统计图中,“主动质疑”对应的圆心角为 度;
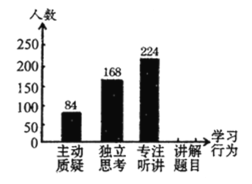
(3)请补充完整条形统计图;
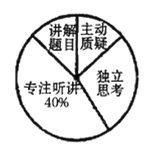
(4)若该市初中学生共有![]() 万人,在课堂上具有“独立思考”行为的学生约有多少人?
万人,在课堂上具有“独立思考”行为的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别写有数字-1,1,2的卡片,它们除数字不同无其它差别,现将这三张卡片背面朝上洗匀后.
(1)随机抽取一张,求抽到数字2的概率;
(2)先随机抽取一张,以其正面数字作为k值,将卡片放回再随机抽一张,以其正面的数字作为b值,请你用恰当的方法表示所有可能的结果,并求出直线y=kx+b的图像不经过第四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
张老师给爱好学习的小军和小俊提出这样的一个问题:如图1,在△ABC中,AB=AC,点P为边BC上任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D,E,过点C作CF⊥AB,垂足为F,求证:PD+PE=CF.
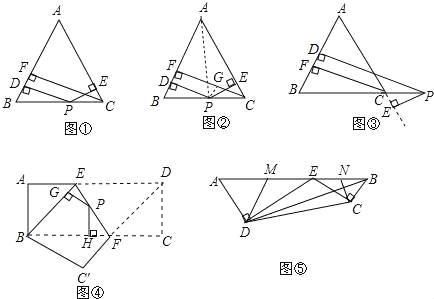
小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为G,可以证得:PD=GF,PE=CG,则PD+PE=CF.
[变式探究]
如图3,当点P在BC延长线上时,其余条件不变,求证:PD﹣PE=CF;
请运用上述解答中所积累的经验和方法完成下列两题:
[结论运用]
如图4,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;
[迁移拓展]
图5是一个航模的截面示意图.在四边形ABCD中,E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为D、C,且ADCE=DEBC,AB=2![]() dm,AD=3dm,BD=
dm,AD=3dm,BD=![]() dm.M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.
dm.M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() 为
为![]() 的内接四边形,直径
的内接四边形,直径![]() 与对角线
与对角线![]() 相交于点
相交于点![]() ,作
,作![]() 于
于![]() ,
,![]() 与过
与过![]() 点的直线相交于点
点的直线相交于点![]() ,
,![]() .
.
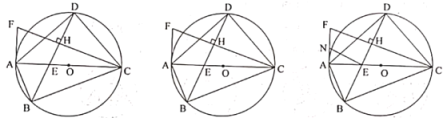
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)若![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,若
,若![]() ,
,![]() 的半径为
的半径为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金松科技生态农业养殖有限公司种植和销售一种绿色羊肚菌,已知该羊肚菌的成本是12元/千克,规定销售价格不低于成本,又不高于成本的两倍.经过市场调查发现,某天该羊肚菌的销售量y(千克)与销售价格x(元/千克)的函数关系如下图所示:
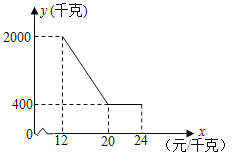
(1)求y与x之间的函数解析式;
(2)求这一天销售羊肚菌获得的利润W的最大值;
(3)若该公司按每销售一千克提取1元用于捐资助学,且保证每天的销售利润不低于3600元,问该羊肚菌销售价格该如何确定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P、Q分别从点A、B同时开始移动,点P的速度为1 cm/秒,点Q的速度为2 cm/秒,点Q移动到点C后停止,点P也随之停止运动下列时间瞬间中,能使△PBQ的面积为15cm 的是( )
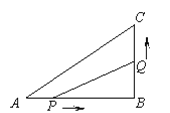
A. 2秒钟 B. 3秒钟 C. 4秒钟 D. 5秒钟
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com