
【题目】金松科技生态农业养殖有限公司种植和销售一种绿色羊肚菌,已知该羊肚菌的成本是12元/千克,规定销售价格不低于成本,又不高于成本的两倍.经过市场调查发现,某天该羊肚菌的销售量y(千克)与销售价格x(元/千克)的函数关系如下图所示:
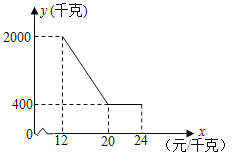
(1)求y与x之间的函数解析式;
(2)求这一天销售羊肚菌获得的利润W的最大值;
(3)若该公司按每销售一千克提取1元用于捐资助学,且保证每天的销售利润不低于3600元,问该羊肚菌销售价格该如何确定.
【答案】(1)y![]() ;(2)5000元;(3)销售价格确定为16≤x≤19或22≤x≤24
;(2)5000元;(3)销售价格确定为16≤x≤19或22≤x≤24
【解析】
(1)①当12≤x≤20时,设y=kx+b.代(12,2000),(20,400),求得k和b;②当20<x≤24时,y=400;
(2)分别写出①当12≤x≤20时,②当20<x≤24时,相应的函数关系式并求得其最大值,两者相比较,取较大者即可;
(3)分两种情况:①当12≤x≤20时,②当20<x≤24时,分别令其W值等于或者大于等于3600,即可得解.
解:(1)①当12≤x≤20时,设y=kx+b.代(12,2000),(20,400),
得![]()
解得![]()
∴y=﹣200x+4400
②当20<x≤24时,y=400.
综上,y=![]()
(2)①当12≤x≤20时,
W=(x﹣12)y
=(x﹣12)(﹣200x+4400)
=﹣200(x﹣17)2+5000
当x=17时,W的最大值为5000;
②当20<x≤24时,
W=(x﹣12)y
=400x﹣4800.
当x=24时,W的最大值为4800.
∴最大利润为5000元.
(3)①当12≤x≤20时,
W=(x﹣12﹣1)y
=(x﹣13)(﹣2000x+4400)
=﹣200(x﹣17.5)2+4050
令﹣200(x﹣17.5)2+4050=3600
x1=16,x2=19
∴定价为16≤x≤19
②当20<x≤24时,
W=400(x﹣13)=400x﹣5200≥3600
∴22≤x≤24.
综上,销售价格确定为16≤x≤19或22≤x≤24.


科目:初中数学 来源: 题型:
【题目】任大叔决定在承包的荒山上种樱桃树,第一次用1000元购进了一批树苗,第二次又用1000元购进该种树苗,但这次每棵树苗的进价是第一次进价的2倍,购进数量比第次少了100棵;
(1)求第一次每棵树苗的进价是多少元?
(2)一年后,树苗的成活率为85%,每棵樱桃树平均产樱桃30斤,任大叔将两批樱桃树所产樱桃按同一价格全部销售完毕后,获利不低于89800元,求每斤樱桃的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (a≠0)的图象如图所示,则下列命题中正确的是( )
(a≠0)的图象如图所示,则下列命题中正确的是( )
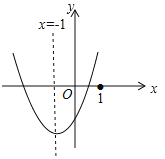
A. a >b>c
B. 一次函数y=ax +c的图象不经第四象限
C. m(am+b)+b<a(m是任意实数)
D. 3b+2c>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象相交于点A(1,4)和B(﹣2,n).
的图象与一次函数y2=ax+b的图象相交于点A(1,4)和B(﹣2,n).

(1)求反比例函数与一次函数的解析式;
(2)请根据图象直接写出y1<y2时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,E是AC中点.
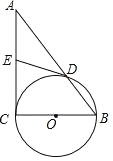
(1)求证:DE是⊙O的切线;
(2)若AB=10,BC=6,连接CD,OE,交点为F,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
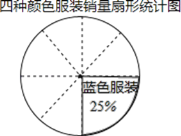
【题目】某超市销售多种颜色的运动服装,其中平均每天销售红、黄、蓝、白四种颜色运动服的数量如表,由此绘制的不完整的扇形统计图如图:
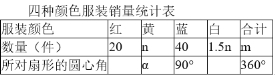
(1)求表中m、n、α的值,并将扇形统计图补充完整:表中m= ,n= ,α= ;
(2)为吸引更多的顾客,超市将上述扇形统计图制成一个可自由转动的转盘,并规定:顾客在本超市购买商品金额达到一定的数目,就获得一次转动转盘的机会.如果转盘停止后,指针指向红色服装区域、黄色服装区域,可分别获得60元、20元的购物券.求顾客每转动一次转盘获得购物券金额的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
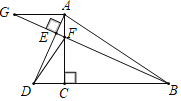
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=4,sin∠ABC=![]() ,点D为射线BC上一点,联结AD,过点B作BE⊥AD分别交射线AD、AC于点E、F,联结DF,过点A作AG∥BD,交直线BE于点G.
,点D为射线BC上一点,联结AD,过点B作BE⊥AD分别交射线AD、AC于点E、F,联结DF,过点A作AG∥BD,交直线BE于点G.
(1)当点D在BC的延长线上时,如果CD=2,求tan∠FBC;
(2)当点D在BC的延长线上时,设AG=x,S△DAF=y,求y关于x的函数关系式(不需要写函数的定义域);
(3)如果AG=8,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
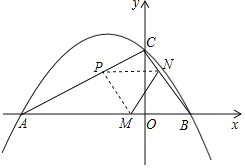
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣3,0)、B两点,与y轴相交于点![]() .当x=﹣4和x=2时,二次函数y=ax2+bx+c(a≠0)的函数值y相等,连接AC,BC.
.当x=﹣4和x=2时,二次函数y=ax2+bx+c(a≠0)的函数值y相等,连接AC,BC.
(1)求抛物线的解析式;
(2)判断△ABC的形状,并说明理由;
(3)若点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC边运动,其中一个点到达终点时,另一点也随之停止运动,当运动时间为t秒时,连接MN,将△BMN沿MN翻折,B点恰好落在AC边上的P处,则t的值为 ,点P的坐标为 ;
(4)抛物线对称轴上是否存在一点F,使得△ACF是以AC为直角边的直角三角形?若不存在,请说明理由;若存在,请直接写出点F的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com