
����Ŀ���ۺ���̽��
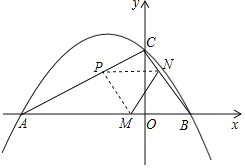
��ͼ��������y��ax2+bx+c��a��0����x�ύ��A����3��0����B���㣬��y���ཻ�ڵ�![]() ����x����4��x��2ʱ�����κ���y��ax2+bx+c��a��0���ĺ���ֵy��ȣ�����AC��BC��
����x����4��x��2ʱ�����κ���y��ax2+bx+c��a��0���ĺ���ֵy��ȣ�����AC��BC��
��1���������ߵĽ���ʽ��
��2���жϡ�ABC����״����˵�����ɣ�
��3������M��Nͬʱ��B�����������ÿ��1����λ���ȵ��ٶȷֱ���BA��BC���˶�������һ���㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt��ʱ������MN������BMN��MN���ۣ�B��ǡ������AC���ϵ�P������t��ֵΪ�� ������P������Ϊ�� ����
��4�������߶Գ������Ƿ����һ��F��ʹ�á�ACF����ACΪֱ�DZߵ�ֱ�������Σ��������ڣ���˵�����ɣ������ڣ���ֱ��д����F�����꣮
���𰸡���1��![]() ����2����ABC��ֱ�������Σ����ɼ���������3��
����2����ABC��ֱ�������Σ����ɼ���������3��![]() ��
��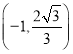 ����4�����ڣ�F1
����4�����ڣ�F1![]() ��F2
��F2![]() ��
��
��������
��1���ɶԳ����������B�����꣬���������ߵĽ���ʽΪy=a(x+3)(x��1)����C�������y=a(x+3)(x��1)���ɣ�
��2�����жϡ�ABCΪֱ�������Σ��ֱ����AB��AC��BC�ij����ɹ��ɶ������涨����֤�����ۣ�
��3����Ϊ��M��Nͬʱ��B�����������ÿ��1����λ���ȵ��ٶȷֱ���BA��BC���˶�������BM=BN=t��֤�ı���PMBN�����Σ���PM��y�ύ��H��֤��CPN�ס�CAB�������������ε����ʿ����t��ֵ��CH�ij����ɵó���P�����꣬���ֱ��AC�Ľ���ʽ������P��������뼴�ɣ�
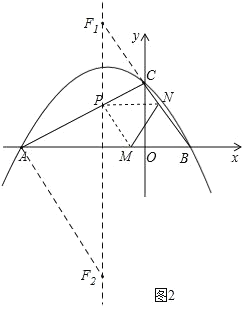
��4�����ֱ��BC�Ľ���ʽ����ͼ2������ACF=90��ʱ����B��C��F��һ��ֱ���ϣ����ֱ��BC��Գ���Ľ��㼴�ɣ�����CAF=90��ʱ�����ֱ��AF�Ľ���ʽ����������Գ���Ľ��㼴�ɣ�
��1������������y=ax2+bx+c�У���x=��4��x=2ʱ�����κ���y=ax2+bx+c�ĺ���ֵy��ȣ�
�������ߵĶԳ���Ϊx![]() 1��
1��
�֡�������y=ax2+bx+c��x�ύ��A(��3��0)��B���㣬
�ɶԳ��Կ�֪B(1��0)��
����������ߵĽ���ʽΪy=a(x+3)(x��1)��
��C(0��![]() )����y=a(x+3)(x��1)��
)����y=a(x+3)(x��1)��
���3a![]() ��
��
��ã�a![]() ��
��
��������ߵĽ���ʽΪy![]() (x+3)(x��1)
(x+3)(x��1)![]() x2
x2![]() x
x![]() ��
��
��2����ABCΪֱ�������Σ��������£�
��A(��3��0)��B(1��0)��C(0��![]() )��
)��
��OA=3��OB=1��OC![]() ��
��
��AB=OA+OB=4��AC![]() 2
2![]() ��BC
��BC![]() 2��
2��
��AC2+BC2=16��AB2=16��
��AC2+BC2=AB2��
���ABC��ֱ�������Σ�
��3���ߵ�M��Nͬʱ��B�����������ÿ��1����λ���ȵ��ٶȷֱ���BA��BC���˶���
��BM=BN=t��
�ɷ���֪����BMN�ա�PMN��
��BM=PM=BN=PN=t��
���ı���PMBN�����Σ�
��PN��AB��
���CPN�ס�CAB����PM��y�ύ��H��
��![]() ��
��
��![]() ��
��
��ã�t![]() ��CH
��CH![]() ��
��
��OH=OC��CH![]() ��
��
��yP![]() ��
��
��ֱ��AC�Ľ���ʽΪy=kx![]() ��
��
����A(��3��0)����y=kx![]() ��
��
�ã�k![]() ��
��
��ֱ��AC�Ľ���ʽΪy![]() x
x![]() ��
��
��yP![]() ����y
����y![]() x
x![]() ��
��
��x=��1��
��P(��1��![]() )��
)��
�ʴ�Ϊ��![]() ��(��1��
��(��1��![]() )��
)��
��4����ֱ��BC�Ľ���ʽΪy=kx![]() ��
��
����B(1��0)����y=kx![]() ��
��
�ã�k![]() ��
��
��ֱ��BC�Ľ���ʽΪy![]() x
x![]() ��
��
�ɣ�2��֪��ABCΪֱ�������Σ���ACB=90�㣮
����ͼ2������ACF=90��ʱ����B��C��F��һ��ֱ���ϣ�
��y![]() x
x![]() �У���x=��1ʱ��y=2
�У���x=��1ʱ��y=2![]() ��
��
��F1(��1��2![]() )��
)��
�ڵ���CAF=90��ʱ��AF��BC��
�����ֱ��AF�Ľ���ʽΪy![]() x+n��
x+n��
����A(��3��0)����y![]() x+n��
x+n��
�ã�n=��3![]() ��
��
��ֱ��AF�Ľ���ʽΪy![]() x��3
x��3![]() ��
��
��y![]() x��3
x��3![]() �У���x=��1ʱ��y=��2
�У���x=��1ʱ��y=��2![]() ��
��
��F2(��1����2![]() )��
)��
������������F������ΪF1(��1��2![]() )��F2(��1����2
)��F2(��1����2![]() )��
)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ɿƼ���̬ũҵ��ֳ����˾��ֲ������һ����ɫ��Ǿ�����֪����Ǿ��ijɱ���12Ԫ/ǧ�ˣ��涨���ۼ۸��ڳɱ����ֲ����ڳɱ��������������г����鷢�֣�ij�����Ǿ���������y��ǧ�ˣ������ۼ۸�x��Ԫ/ǧ�ˣ��ĺ�����ϵ����ͼ��ʾ��
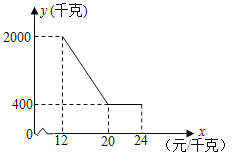
��1����y��x֮��ĺ�������ʽ��
��2������һ��������Ǿ���õ�����W�����ֵ��
��3�����ù�˾��ÿ����һǧ����ȡ1Ԫ���ھ�����ѧ���ұ�֤ÿ�������������3600Ԫ���ʸ���Ǿ����ۼ۸�����ȷ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ABC��90�㣬AB��8cm��BC��6cm������P��Q�ֱ�ӵ�A��Bͬʱ��ʼ�ƶ�����P���ٶ�Ϊ1 cm���룬��Q���ٶ�Ϊ2 cm���룬��Q�ƶ�����C��ֹͣ����PҲ��ֹ֮ͣ�˶�����ʱ��˲���У���ʹ��PBQ�����Ϊ15cm ���ǣ� ��
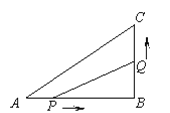
A. 2���� B. 3���� C. 4���� D. 5����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
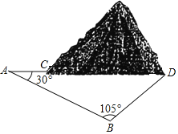
����Ŀ��2019��11��26�գ�³�ϸ�����ʽ��ͨ��Ӫ��³�ϸ������ʶ�����������Ҫ����һ��Сɽ����ͼ��ʩ�����ƻ���AC������������Ϊ�˼ӿ�ʩ���ٶȣ�Ҫ��Сɽ����һ��D��A��C��D���ߣ���ͬʱʩ������á�CAB��30�㣬 ����ABD��105�㣬��AD�ij���
����ABD��105�㣬��AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧ�ļס�������ͬѧ����һ��������Ϸ���ó���������д�����֩�1��0��1�ұ�����ȫ��ͬ�Ŀ�Ƭ���������ſ�Ƭ���泯��ϴ�Ⱥ��������ȡһ�ţ�������������Ϊp��ֵ��Ȼ��Ƭ�Żز�ϴ�ȣ����ٴ������ſ�Ƭ�������ȡһ�ţ�������������Ϊqֵ�����ν����Ϊ![]() ��
��
��1���������������״ͼ���б�����ʾ![]() ���п��ܳ��ֵĽ����
���п��ܳ��ֵĽ����
��2�����������x�ķ���![]() û��ʵ�����ĸ��ʣ�
û��ʵ�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������ʦ�����Ķ�����ijУͼ��ݵIJ����2016���2018�����������5������ӵ�7.2���.
��1����������������������ʣ�
��2����ͳ��֪������ŵ������IJ�����2016���ռ��ʱ����������5.6%���������������ӵ�ͼ���У�����ŵ�������ռ�İٷ���ǡ�õ���������������������ʣ���ô��2018�������ŵ������IJ���ռ���������İٷ�֮����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У���֪��A��8��0���͵�B��0��6������C��AB���е㣬��P������AOB�ϣ�ֱ��CP�ء�AOB�����õ����������AOB���ƣ���ô��P��������_____��
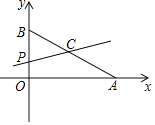
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijУ�������ĸ��С�飺![]() �����֣�
�����֣�![]() ��������
��������![]() ���赸��
���赸��![]() ���黭��Ϊ�˽�ѧ�����ĸ��С���ϲ����������ѡȡ��У����ѧ�����е��飬Ҫ��ÿ��ѧ�����б���ѡ�����ֻ��ѡ��һ��С�飬���ݵ�������������������������ͳ��ͼ��
���黭��Ϊ�˽�ѧ�����ĸ��С���ϲ����������ѡȡ��У����ѧ�����е��飬Ҫ��ÿ��ѧ�����б���ѡ�����ֻ��ѡ��һ��С�飬���ݵ�������������������������ͳ��ͼ��
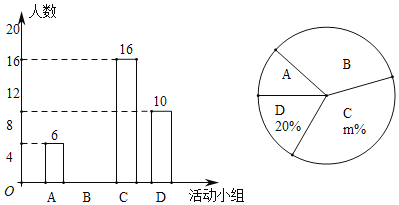
����ͼ��������Ϣ������������⣺
��1�����γ������鹲������� ����ѧ��������ͳ��ͼ�е�![]() ֵ���� ����
ֵ���� ����
��2���벹ȫ����ͳ��ͼ��
��3��ϲ�����黭����ѧ��������������������Ů�������ر����㣬�ִ���4�������ѡȡ���˲μӱ����������б�����״ͼ�ķ��������ѡ������ǡ����һ��������һ��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() ����������ֱ�Ϊ
����������ֱ�Ϊ![]() ��
��![]() ��
��![]() ����
����![]() ��
��
��1���Ե�![]() Ϊλ�����ģ��ڵ�һ�����ڻ���
Ϊλ�����ģ��ڵ�һ�����ڻ���![]() ��λ��ͼ��
��λ��ͼ��![]() ����
����![]() ��
��![]() �����Ʊ�Ϊ
�����Ʊ�Ϊ![]() ��д����
��д����![]() �����ꣻ
�����ꣻ
��2��![]() �е�һ��
�е�һ��![]() �ڣ�1����λ�Ʊ任���Ӧ
�ڣ�1����λ�Ʊ任���Ӧ![]() �еĵ�
�еĵ�![]() ����ֱ��д����
����ֱ��д����![]() �����꣮���ú�
�����꣮���ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
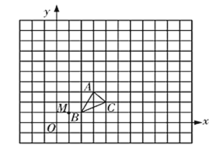
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com