
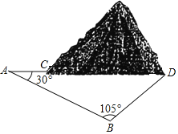
【题目】2019年11月26日,鲁南高铁正式开通运营.鲁南高铁临沂段修建过程中需要经过一座小山.如图,施工方计划沿AC方向挖隧道,为了加快施工速度,要在小山的另一侧D(A、C、D共线)处同时施工.测得∠CAB=30°,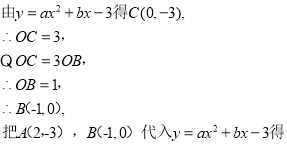 ,∠ABD=105°,求AD的长.
,∠ABD=105°,求AD的长.
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象相交于点A(1,4)和B(﹣2,n).
的图象与一次函数y2=ax+b的图象相交于点A(1,4)和B(﹣2,n).

(1)求反比例函数与一次函数的解析式;
(2)请根据图象直接写出y1<y2时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
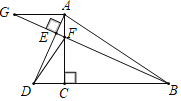
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=4,sin∠ABC=![]() ,点D为射线BC上一点,联结AD,过点B作BE⊥AD分别交射线AD、AC于点E、F,联结DF,过点A作AG∥BD,交直线BE于点G.
,点D为射线BC上一点,联结AD,过点B作BE⊥AD分别交射线AD、AC于点E、F,联结DF,过点A作AG∥BD,交直线BE于点G.
(1)当点D在BC的延长线上时,如果CD=2,求tan∠FBC;
(2)当点D在BC的延长线上时,设AG=x,S△DAF=y,求y关于x的函数关系式(不需要写函数的定义域);
(3)如果AG=8,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(﹣3,0),其对称轴为直线x=﹣![]() ,结合图象分析下列结论:①abc>0;②3a+c>0;③当x<0时,y随x的增大而增大:④若m,n(m<n)为方程a(x+3)(x﹣2)+3=0的两个根,则m<﹣3且n>2;⑤
,结合图象分析下列结论:①abc>0;②3a+c>0;③当x<0时,y随x的增大而增大:④若m,n(m<n)为方程a(x+3)(x﹣2)+3=0的两个根,则m<﹣3且n>2;⑤![]() <0,其中正确的结论有( )
<0,其中正确的结论有( )
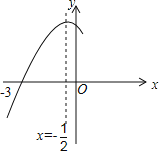
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
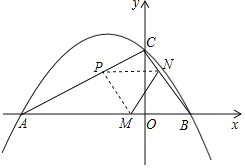
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣3,0)、B两点,与y轴相交于点![]() .当x=﹣4和x=2时,二次函数y=ax2+bx+c(a≠0)的函数值y相等,连接AC,BC.
.当x=﹣4和x=2时,二次函数y=ax2+bx+c(a≠0)的函数值y相等,连接AC,BC.
(1)求抛物线的解析式;
(2)判断△ABC的形状,并说明理由;
(3)若点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC边运动,其中一个点到达终点时,另一点也随之停止运动,当运动时间为t秒时,连接MN,将△BMN沿MN翻折,B点恰好落在AC边上的P处,则t的值为 ,点P的坐标为 ;
(4)抛物线对称轴上是否存在一点F,使得△ACF是以AC为直角边的直角三角形?若不存在,请说明理由;若存在,请直接写出点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一组密码的一部分.为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“今年考试”的真实意思是“努力发挥”.若“今”所处的位置为(x,y),你找到的密码钥匙是 ,破译“正做数学”的真实意思是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com