
【题目】如图,在△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,E是AC中点.
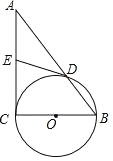
(1)求证:DE是⊙O的切线;
(2)若AB=10,BC=6,连接CD,OE,交点为F,求OF的长.
【答案】(1)见解析;(2)OF=1.8
【解析】
(1)由题意连接CD、OD,求得![]() 即可证明DE是⊙O的切线;
即可证明DE是⊙O的切线;
(2)根据题意运用切线的性质、角平分线性质和勾股定理以及三角形的面积公式进行综合分析求解.
解:(1)证明:连接CD,OD
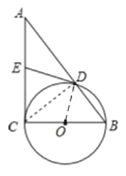
∵∠ACB=90°,BC为⊙O直径,
∴∠BDC=∠ADC=90°,
∵E为AC中点,
∴EC=ED=AE,
∴∠ECD=∠EDC;
又∵∠OCD=∠CDO,
∴![]() ∠EDC+∠CDO=∠ECD+ ∠OCD= ∠ACB=90°,
∠EDC+∠CDO=∠ECD+ ∠OCD= ∠ACB=90°,
∴DE是⊙O的切线.
(2)解:连接CD,OE,
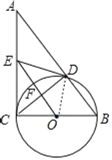
∵∠ACB=90°,
∴AC为⊙O的切线,
∵DE是⊙O的切线,
∴EO平分∠CED,
∴OE⊥CD,F为CD的中点,
∵点E、O分别为AC、BC的中点,
∴OE=![]() AB=
AB=![]() =5,
=5,
在Rt△ACB中,∠ACB=90°,AB=10,BC=6,由勾股定理得:AC=8,
∵在Rt△ADC中,E为AC的中点,
∴DE=![]() AC=
AC=![]() =4,
=4,
在Rt△EDO中,OD=![]() BC=
BC=![]() =3,DE=4,由勾股定理得:OE=5,
=3,DE=4,由勾股定理得:OE=5,
由三角形的面积公式得:S△EDO=![]() ,
,
即4×3=5×DF,
解得:DF=2.4,
在Rt△DFO中,由勾股定理得:OF=![]() =
=![]() =1.8.
=1.8.


科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系中,点A(2,﹣1),B(3,2),C(1,0).解答问题:请按要求对△ABC作如下变换.
(1)将△ABC绕点O逆时针旋转90°得到△A1B1C1;
(2)以点O为位似中心,位似比为2:1,将△ABC在位似中心的异侧进行放大得到△A2B2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
张老师给爱好学习的小军和小俊提出这样的一个问题:如图1,在△ABC中,AB=AC,点P为边BC上任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D,E,过点C作CF⊥AB,垂足为F,求证:PD+PE=CF.
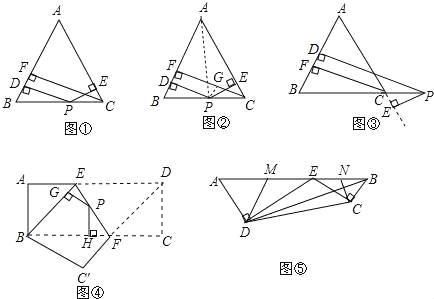
小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为G,可以证得:PD=GF,PE=CG,则PD+PE=CF.
[变式探究]
如图3,当点P在BC延长线上时,其余条件不变,求证:PD﹣PE=CF;
请运用上述解答中所积累的经验和方法完成下列两题:
[结论运用]
如图4,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;
[迁移拓展]
图5是一个航模的截面示意图.在四边形ABCD中,E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为D、C,且ADCE=DEBC,AB=2![]() dm,AD=3dm,BD=
dm,AD=3dm,BD=![]() dm.M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.
dm.M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC的顶角∠A=36°,若将其绕点C顺时针旋转36°,得到△![]() ,点B′在AB边上,
,点B′在AB边上,![]() 交AC于E,连接AA′.有下列结论:①△ABC≌△
交AC于E,连接AA′.有下列结论:①△ABC≌△![]() ;②四边形
;②四边形![]() 是平行四边形;③图中所有的三角形都是等腰三角形;其中正确的结论是( )
是平行四边形;③图中所有的三角形都是等腰三角形;其中正确的结论是( )
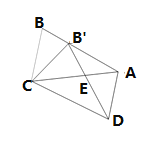
A.①②B.① ③C.②③D.① ② ③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金松科技生态农业养殖有限公司种植和销售一种绿色羊肚菌,已知该羊肚菌的成本是12元/千克,规定销售价格不低于成本,又不高于成本的两倍.经过市场调查发现,某天该羊肚菌的销售量y(千克)与销售价格x(元/千克)的函数关系如下图所示:
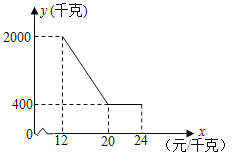
(1)求y与x之间的函数解析式;
(2)求这一天销售羊肚菌获得的利润W的最大值;
(3)若该公司按每销售一千克提取1元用于捐资助学,且保证每天的销售利润不低于3600元,问该羊肚菌销售价格该如何确定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( )

A. abc<0 B. -3a+c<0
C. b2-4ac≥0 D. 将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.
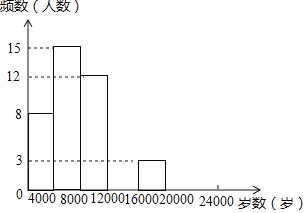
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了满足师生的阅读需求,某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册.
(1)求这两年藏书的年均增长率;
(2)经统计知:中外古典名著的册数在2016年底仅占当时藏书总量的5.6%,在这两年新增加的图书中,中外古典名著所占的百分率恰好等于这两年藏书的年均增长率,那么到2018年底中外古典名著的册数占藏书总量的百分之几?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com