
【题目】如图,在△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( )
A.50°
B.51°
C.51.5°
D.52.5°
【答案】D
【解析】解:∵AC=CD=BD=BE,∠A=50°,
∴∠A=∠CDA=50°,∠B=∠DCB,∠BDE=∠BED.
∵∠B+∠DCB=∠CDA=50°,
∴∠B=25°.
∵∠B+∠EDB+∠DEB=180°,
∴∠BDE=∠BED= ![]() ×(180°-25°)=77.5°.
×(180°-25°)=77.5°.
∴∠CDE=180°-∠CDA-∠BDE=180°-50°-77.5°=52.5° 。
故应选 :D 。
根据等边对等角得出∠A=∠CDA=50°,∠B=∠DCB,∠BDE=∠BED,根据三角形的外角性质得出∠B+∠DCB=∠CDA=50°,从而得出∠B=25°,根据三角形的内角和得出∠B+∠EDB+∠DEB=180°,从而得出∠BDE=∠BED= ![]() ×(180°-25°)=77.5°,根据角的和差得出答案。
×(180°-25°)=77.5°,根据角的和差得出答案。


科目:初中数学 来源: 题型:
【题目】为了调查某校学生的视力情况,在全校的800名学生中随机抽取了80名学生,下列说法正确的是( )
A.此次调查属于全面调查B.样本容量是80
C.800名学生是总体D.被抽取的每一名学生称为个体
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班级第4组第5排位置可以用数对(4,5)表示,则数对(2,3)表示的位置是( )
A. 第3组第2排 B. 第3组第1排 C. 第2组第3排 D. 第2组第2排
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.44°
B.66°
C.88°
D.92°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点B,C,E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )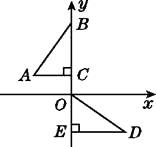
A.△ABC绕点C顺时针旋转90°,再向下平移3个单位长度
B.△ABC绕点C顺时针旋转90°,再向下平移1个单位长度
C.△ABC绕点C逆时针旋转90°,再向下平移1个单位长度
D.△ABC绕点C逆时针旋转90°,再向下平移3个单位长度
查看答案和解析>>
科目:初中数学 来源: 题型:
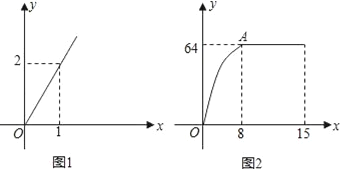
【题目】麻城市思源实验学校自从开展“高效课堂”模式以来,在课堂上进行当堂检测效果很好.每节课40分钟教学,假设老师用于精讲的时间x(单位:分钟)与学生学习收益量y的关系如图1所示,学生用于当堂检测的时间x(单位:分钟)与学生学习收益y的关系如图2所示(其中OA是抛物线的一部分,A为抛物线的顶点),且用于当堂检测的时间不超过用于精讲的时间.
(1)求老师精讲时的学生学习收益量y与用于精讲的时间x之间的函数关系式;
(2)求学生当堂检测的学习收益量y与用于当堂检测的时间x的函数关系式;
(3)问此“高效课堂”模式如何分配精讲和当堂检测的时间,才能使学生在这40分钟的学习收益总量最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com