
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,��B,C,E��y����,Rt��ABC�����任�õ�Rt��ODE,����C������Ϊ(0,1),AC=2,�����ֱ任������( )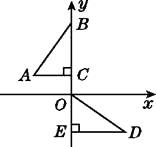
A.��ABC�Ƶ�C˳ʱ����ת90��,������ƽ��3����λ����
B.��ABC�Ƶ�C˳ʱ����ת90��,������ƽ��1����λ����
C.��ABC�Ƶ�C��ʱ����ת90��,������ƽ��1����λ����
D.��ABC�Ƶ�C��ʱ����ת90��,������ƽ��3����λ����

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е����в��ʺϳ����������( )
A.����ij����һ���ڵĿ�����;B.�˽�ȫ��ʳ�μӵ����;
C.����ijС����Ʒ�ֵķ�ѿ��;D.����ij��ѧ�������г���ѧ���;
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ڡ�ABC��,DΪAB��һ��,EΪBC��һ��,��AC=CD=BD=BE,��A=50��,���CDE�Ķ���Ϊ( )
A.50��
B.51��
C.51.5��
D.52.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��,�ڡ�ABC��,AB=AC,��D��BC���е�,��E��AD��.
��1����֤:BE=CE.
��2����ͼ��,��BE���ӳ��߽�AC�ڵ�F,��BF��AC,����ΪF,AF=BF,ԭ����������������.��֤:��AEF�ա�BCF.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y=3x��2��ͼ����������A����1��y1����B����2��y2������y1��y2�Ĵ�С��ϵΪ��������
A. y1��y2 B. y1��y2 C. y1=y2 D. ����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x-3��һ������ʽ�ij˻�Ϊx2+x-12�����������ʽΪ����
A.x+4B.x-4C.x-9D.x+6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������:��ͼ��,��E,F�ֱ���������ABCD�ı�BC,CD��,��EAF=45��,���ж�BE,EF,FD֮���������ϵ.
��1��������֤����
С�ϰѡ�ABE�Ƶ�A��ʱ����ת90������ADG��λ��,�Ӷ�����EF=BE+FD,��������ͼ��֤����������.
��2����������
��ͼ��,���ı���ABCD��,��BAD��90��,AB=AD,��B+��D=180��,��E,F�ֱ��ڱ�BC,CD��,��EAF���BAD������ϵʱ,����EF=BE+FD.��˵������.
��3����̽��Ӧ�á�
��ͼ��,��ij����ͬһˮƽ����,����ͨ��Χ���ı���ABCD.��֪AB=AD=80 m,��B=60��,��ADC=120��,��BAD=150��,��·BC,CD�Ϸֱ��о���E,F,��AE��AD,DF=40( ![]() -1)m,��Ҫ��E,F֮����һ����ֱ�ĵ�·,��������·EF�ij�(�����ȷ��1 m,�ο�����:
-1)m,��Ҫ��E,F֮����һ����ֱ�ĵ�·,��������·EF�ij�(�����ȷ��1 m,�ο�����: ![]() ��1.41,
��1.41, ![]() ��1.73).
��1.73).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������2015�괺��ʮ�ֻ𱬵�һ��������ij��ҵ��4000��ְ�������������ȡ350�ˣ�������ֲ��Ͷԡ������������̬����������˵��飬�������������������ͳ��ͼ������ͳ��ͼ��

��1����ε����У����ְ���������λ������������ô�����λ�����ڵ����������һ�Σ�
��2������Ѷԡ������������̬���еġ�����������������͡�ż�������������ͳ��Ϊ�����������������ô��ν��ܵ����ְ���С�������������������Ƕ��٣�
��3������Ƹ���ҵ���Ӳ�������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����д����ҵı���������ʽ�ֽ���ǣ� ��
A.x2+5x��1=x��x+5����1
B.x2��9=��x+3����x��3��
C.x2��4+3x=��x+2����x��2��+3x
D.��x+2����x��2��=x2��4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com