
【题目】问题:如图①,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
(1)【发现证明】
小聪把△ABE绕点A逆时针旋转90°至△ADG的位置,从而发现EF=BE+FD,请你利用图①证明上述结论.
(2)【类比引申】
如图②,在四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E,F分别在边BC,CD上,则当∠EAF与∠BAD满足关系时,仍有EF=BE+FD.请说明理由.
(3)【探究应用】
如图③,在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80 m,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC,CD上分别有景点E,F,且AE⊥AD,DF=40( ![]() -1)m,现要在E,F之间修一条笔直的道路,求这条道路EF的长(结果精确到1 m,参考数据:
-1)m,现要在E,F之间修一条笔直的道路,求这条道路EF的长(结果精确到1 m,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73).
≈1.73).
【答案】
(1)解:证明:由旋转的性质可得AE=AG,BE=DG,∠B=∠ADG=90°, ∠EAG=90°.
∵∠B+∠ADC=180°,
∴∠ADC+∠ADG=180°.
∴G,D,C三点共线.
∵∠EAF=45°,∴∠GAF=45°,
∴∠GAF=∠EAF.
又∵AF=AF,∴△AFG≌△AFE(SAS).
∴GF=EF.
∵GF=DG+FD=BE+FD,
∴EF=BE+FD
(2)解:∠EAF= ![]() ∠BAD;如图①,
∠BAD;如图①,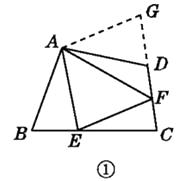
将△ABE绕点A逆时针旋转至△ADG的位置,由旋转的性质可得AE=AG,BE=DG,∠B=∠ADG, ∠BAE=∠DAG.
∵∠B+∠ADC=180°,∴∠ADC+∠ADG=180°.
∴G,D,C三点共线.
∵∠BAE=∠DAG,∴∠BAD=∠EAG.
∵∠EAF= ![]() ∠BAD,∴∠GAF=∠EAF.
∠BAD,∴∠GAF=∠EAF.
又∵AF=AF,∴△AFG≌△AFE(SAS).
∴GF=EF.
∵GF=DG+FD=BE+FD,∴EF=BE+FD.
故答案为∠EAF= ![]() ∠BAD.
∠BAD.
(3)解:∵AE⊥AD,∴∠DAE=90°.
∵∠BAD=150°,∴∠BAE=60°.
又∵∠B=60°,∴△ABE是等边三角形.
∴BE=AB=80 m.
如图②,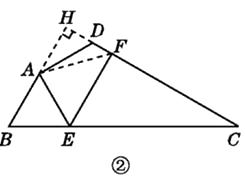
连接AF,过点A作AH⊥CD交CD的延长线于H.
在Rt△AHD中,∠ADH=180°-∠ADC=60°,AD=80 m,
∴∠HAD=30°.
∴HD= ![]() AD=40 m,∴AH=
AD=40 m,∴AH= ![]() =40
=40 ![]() m.
m.
∵DF=40( ![]() -1) m,∴HF=HD+DF=40+40(
-1) m,∴HF=HD+DF=40+40( ![]() -1)=40
-1)=40 ![]() (m).
(m).
∴在Rt△AHF中,AH=HF,∴∠HAF=45°.∴∠DAF=15°.
∴∠EAF=90°-15°=75°.∴∠EAF= ![]() ∠BAD.
∠BAD.
运用上面的结论可得EF=BE+DF=80+40( ![]() -1)=40+40
-1)=40+40 ![]() ≈109(m).即这条道路EF的长约为109 m.
≈109(m).即这条道路EF的长约为109 m.
【解析】(1)根据旋转的性质可证得AE=AG,BE=DG,∠B=∠ADG=90°, ∠EAG=90°,再根据∠EAF=45°,可证得∠GAF=∠EAF,根据全等三角形的判定证明△AFG≌△AFE,得出GF=EF,然后根据GF=DG+FD,即可证得结论。
(2)将△ABE绕点A逆时针旋转至△ADG的位置,由旋转的性质可得AE=AG,BE=DG,∠B=∠ADG, ∠BAE=∠DAG,可证得∠ADC+∠ADG=180°,得出G,D,C三点共线,再根据∠EAF=![]() ∠BAD去证明∠GAF=∠EAF,从而证得△AFG≌△AFE,得出GF=EF,然后再证明EF=BE+FD,就可得出当∠EAF=
∠BAD去证明∠GAF=∠EAF,从而证得△AFG≌△AFE,得出GF=EF,然后再证明EF=BE+FD,就可得出当∠EAF=![]() ∠BAD时,仍有EF=BE+FD成立。
∠BAD时,仍有EF=BE+FD成立。
(3)结合已知条件易证△ABE是等边三角形.,就可求出BE的长,添加辅助线,连接AF,过点A作AH⊥CD交CD的延长线于H,根据30°角所对的直角边等于斜边的一半求出HD的长,再根据勾股定理求出AH的长,从而就可求出HF的长,证得AH=HF,然后证明∠EAF=![]() ∠BAD,根据以上结论可求出EF的长。
∠BAD,根据以上结论可求出EF的长。


科目:初中数学 来源: 题型:
【题目】为了调查某校学生的视力情况,在全校的800名学生中随机抽取了80名学生,下列说法正确的是( )
A.此次调查属于全面调查B.样本容量是80
C.800名学生是总体D.被抽取的每一名学生称为个体
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点B,C,E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )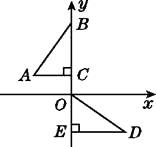
A.△ABC绕点C顺时针旋转90°,再向下平移3个单位长度
B.△ABC绕点C顺时针旋转90°,再向下平移1个单位长度
C.△ABC绕点C逆时针旋转90°,再向下平移1个单位长度
D.△ABC绕点C逆时针旋转90°,再向下平移3个单位长度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用直尺画图(先用铅笔画图,然后再用墨水笔将符合条件的图形画出).
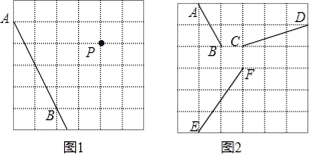
(1)利用图1中的网格,过P点画直线AB的平行线和垂线;
(2)平移图(2)网格中的三条线段AB、CD、EF,使平移后三条线段首尾顺次相接组成一个三角形;
(3)如果每个方格的边长是单位1,那么图(2)中组成的三角形的面积等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线C1:y=x2+4x﹣3与x轴交于A、B两点,将C1向右平移得到C2,C2与x轴交于B、C两点.
(1)求抛物线C2的解析式.
(2)点D是抛物线C2在x轴上方的图象上一点,求S△ABD的最大值.
(3)直线l过点A,且垂直于x轴,直线l沿x轴正方向向右平移的过程中,交C1于点E交C2于点F,当线段EF=5时,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住市文化艺术节的商机,某商店决定购进A,B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,
B种纪念品6件,需要800元.
(1)求购进A,B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
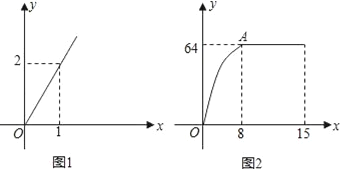
【题目】麻城市思源实验学校自从开展“高效课堂”模式以来,在课堂上进行当堂检测效果很好.每节课40分钟教学,假设老师用于精讲的时间x(单位:分钟)与学生学习收益量y的关系如图1所示,学生用于当堂检测的时间x(单位:分钟)与学生学习收益y的关系如图2所示(其中OA是抛物线的一部分,A为抛物线的顶点),且用于当堂检测的时间不超过用于精讲的时间.
(1)求老师精讲时的学生学习收益量y与用于精讲的时间x之间的函数关系式;
(2)求学生当堂检测的学习收益量y与用于当堂检测的时间x的函数关系式;
(3)问此“高效课堂”模式如何分配精讲和当堂检测的时间,才能使学生在这40分钟的学习收益总量最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com