
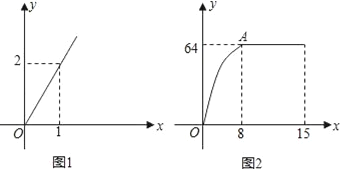
【题目】麻城市思源实验学校自从开展“高效课堂”模式以来,在课堂上进行当堂检测效果很好.每节课40分钟教学,假设老师用于精讲的时间x(单位:分钟)与学生学习收益量y的关系如图1所示,学生用于当堂检测的时间x(单位:分钟)与学生学习收益y的关系如图2所示(其中OA是抛物线的一部分,A为抛物线的顶点),且用于当堂检测的时间不超过用于精讲的时间.
(1)求老师精讲时的学生学习收益量y与用于精讲的时间x之间的函数关系式;
(2)求学生当堂检测的学习收益量y与用于当堂检测的时间x的函数关系式;
(3)问此“高效课堂”模式如何分配精讲和当堂检测的时间,才能使学生在这40分钟的学习收益总量最大?
【答案】(1)老师精讲时的学生学习收益量y与用于精讲的时间x之间的函数关系式为y=2x;
(2)学生当堂检测的学习收益量y与用于当堂检测的时间x的函数关系式为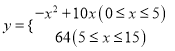 ;
;
(3)老师在课堂用于精讲的时间为33分钟,学生当堂检测的时间为7分钟时,学习收益总量最大.
【解析】(1)由图设该函数解析式为y=kx,即可依题意求出y与x 的函数关系式.
(2)本题涉及分段函数的知识,需要注意的是x的取值范围依照分段函数的解法解出即可.
(3)设学生当堂检测的时间为x分钟(0≤≤15),学生的学习收益总量为W,则老师在课堂用于精讲的时间为(40-x)分钟,用配方法的知识解答该题即可.
解:(1)设y=kx,把(1,2)代入,得k=2.∴y=2x.
自变量x的取值范围是:0≤x≤40.
(2)当0≤x≤8时,设y=a(x-8)2+64,
y=
把(0,0)代入,得64a+64=0,a=-1.
∴y=-(x-8)2+64=-x2+16x.
当8=x=15时,y=64
(3)设学生当堂检测的时间为x分钟(0=x=15),学生的学习收益总量为W,则老师在课堂用于精讲的时间为(40-x)分钟.
当0=x=8时,w=-x2+16x+2(40-x)=-x2+14x+80=-(x-7)2+129.
∴当x=7时,W 最大=129.
当8=x=15时,W=64+2(40-x)=-2x+144.
∵W随x的增大而减小, ∴当x=8时,W最大=128
综合所述,当x=7时,W最大=129,此时40-x=33.
即老师在课堂用于精讲的时间为33分钟,学生当堂检测的时间为7分钟时,学习收益总量最大.

“点睛”本题考查了待定系数法求一次函数的解析式的运用,二次函数的运用,顶点式求二次函数的最大值的运用,解答时求出二次函数的解析式是关键.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( )
A.50°
B.51°
C.51.5°
D.52.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图①,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
(1)【发现证明】
小聪把△ABE绕点A逆时针旋转90°至△ADG的位置,从而发现EF=BE+FD,请你利用图①证明上述结论.
(2)【类比引申】
如图②,在四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E,F分别在边BC,CD上,则当∠EAF与∠BAD满足关系时,仍有EF=BE+FD.请说明理由.
(3)【探究应用】
如图③,在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80 m,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC,CD上分别有景点E,F,且AE⊥AD,DF=40( ![]() -1)m,现要在E,F之间修一条笔直的道路,求这条道路EF的长(结果精确到1 m,参考数据:
-1)m,现要在E,F之间修一条笔直的道路,求这条道路EF的长(结果精确到1 m,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73).
≈1.73).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“抢红包”是2015年春节十分火爆的一项网络活动,某企业有4000名职工,从中随机抽取350人,按年龄分布和对“抢红包”所持态度情况进行了调查,并将调查结果绘成了条形统计图和扇形统计图.

(1)这次调查中,如果职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?
(2)如果把对“抢红包”所持态度中的“经常(抢红包)”和“偶尔(抢红包)”统称为“参与抢红包”,那么这次接受调查的职工中“参与抢红包”的人数是多少?
(3)请估计该企业“从不(抢红包)”的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“震灾无情人有情”.民政局将全市为四川受灾地区捐赠的物资打包成件,其中帐篷和食品共320件,帐篷比食品多80件.
(1)求打包成件的帐篷和食品各多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批帐篷和食品全部运往受灾地区.已知甲种货车最多可装帐篷40件和食品10件,乙种货车最多可装帐篷和食品各20件.则民政局安排甲、乙两种货车时有几种方案?请你帮助设计出来.
(3)在第(2)问的条件下,如果甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元.民政局应选择哪种方案可使运输费最少?最少运输费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列从左到右的变形属于因式分解的是( )
A.x2+5x﹣1=x(x+5)﹣1
B.x2﹣9=(x+3)(x﹣3)
C.x2﹣4+3x=(x+2)(x﹣2)+3x
D.(x+2)(x﹣2)=x2﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在梯形ABCD中,AD∥BC,且AD=4cm,AB=6cm,BC=12cm,DC=10cm.若动点P从A点出发,以每秒4cm的速度沿线段AD、DC向C点运动;动点Q从C点出发以每秒5cm的速度沿CB向B点运动. 当Q点到达B点时,动点P、Q同时停止运动. 设点P、Q同时出发,并运动了t秒.
(1)求梯形ABCD的面积.
(2)当t为何值时,四边形PQCD成为平行四边形?
(3)是否存在t,使得P点在线段DC上,且PQ⊥DC(如图(2)所示)?若存在,求出此时t的值,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com