练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在平面直角坐标系中，点M(a－3，a＋4)，点N(5，9)，若MN∥y轴，则a=____．

    【答案】8

    【解析】

    根据MN∥y轴可得M、N两点的横坐标相等，列出方程即可求得a的值

    解：∵MN∥y轴，

    ∴M、N两点的横坐标相等，

    a-3=5，

    解得：a=8，

    故答案为：8.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某班级第4组第5排位置可以用数对(4，5)表示，则数对(2，3)表示的位置是(　 )

    A. 第3组第2排 B. 第3组第1排 C. 第2组第3排 D. 第2组第2排

    查看答案和解析>>

    科目：初中数学 来源： 题型：

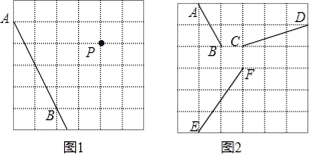
    【题目】利用直尺画图（先用铅笔画图，然后再用墨水笔将符合条件的图形画出）．

    （1）利用图1中的网格，过P点画直线AB的平行线和垂线；

    （2）平移图（2）网格中的三条线段AB、CD、EF，使平移后三条线段首尾顺次相接组成一个三角形；

    （3）如果每个方格的边长是单位1，那么图（2）中组成的三角形的面积等于　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了抓住市文化艺术节的商机，某商店决定购进A，B两种艺术节纪念品．若购进A种纪念品8件，B种纪念品3件，需要950元；若购进A种纪念品5件，

    B种纪念品6件，需要800元．

    （1）求购进A，B两种纪念品每件各需多少元？

    （2）若该商店决定购进这两种纪念品共100件，考虑市场需求和资金周转，用于购买这100件纪念品的资金不少于7500元，但不超过7650元，那么该商店共有几种进货方案？

    （3）若销售每件A种纪念品可获利润20元，每件B种纪念品可获利润30元，在（2）问的各种进货方案中，哪一种方案获利最大？最大利润是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx+c（a≠0）经过点A（﹣3，0）、B（1，0）、C（﹣2，1），交y轴于点M．

    （1）求抛物线的表达式；

    （2）D为抛物线在第二象限部分上的一点，作DE垂直x轴于点E，交线段AM于点F，求线段DF长度的最大值，并求此时点D的坐标；

    （3）抛物线上是否存在一点P，作PN垂直x轴于点N，使得以点P、A、N为顶点的三角形与△MAO相似（不包括全等）？若存在，求点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

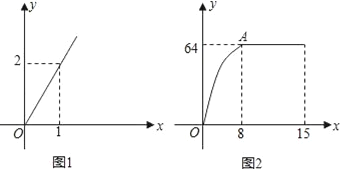
    【题目】麻城市思源实验学校自从开展“高效课堂”模式以来，在课堂上进行当堂检测效果很好．每节课40分钟教学，假设老师用于精讲的时间x（单位：分钟）与学生学习收益量y的关系如图1所示，学生用于当堂检测的时间x（单位：分钟）与学生学习收益y的关系如图2所示（其中OA是抛物线的一部分，A为抛物线的顶点），且用于当堂检测的时间不超过用于精讲的时间．

    （1）求老师精讲时的学生学习收益量y与用于精讲的时间x之间的函数关系式；

    （2）求学生当堂检测的学习收益量y与用于当堂检测的时间x的函数关系式；

    （3）问此“高效课堂”模式如何分配精讲和当堂检测的时间，才能使学生在这40分钟的学习收益总量最大？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个四边形的周长是48厘米，已知第二边长比第一边长的2倍多3厘米，第三边长等于第一边长和第二边长的和，第四边长与第一边长相等．则这个四边形第二边长是（　　）

    A.6厘米B.15厘米C.16厘米D.21厘米

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先化简，再求值：（x+2）2+2（x+2）（x﹣4）﹣（x+3）（x﹣3），其中x=﹣1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=5cm，点D在边BC上，且CD=3cm，现有两个动点P、Q分别从点A和点B同时出发，其中点P以1cm/s的速度沿AC向终点运动；点Q以1.25cm/s的速度沿BC向终点C运动，过点P作PE∥BC交AD于点E，连接EQ，设动点运动时间为ts（0＜t＜4）．

    （1）连接DP，当t＞1时，四边形EQDP能够成为平行四边形吗？请说明理由；

    （2）连接PQ，在运动过程中，不论t取何值，总有PQ与AB平行．为什么？

    （3）当t为何值时，△EDQ为直角三角形？

    查看答案和解析>>

    同步练习册答案