Question

【题目】如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=5cm，点D在边BC上，且CD=3cm，现有两个动点P、Q分别从点A和点B同时出发，其中点P以1cm/s的速度沿AC向终点运动；点Q以1.25cm/s的速度沿BC向终点C运动，过点P作PE∥BC交AD于点E，连接EQ，设动点运动时间为ts（0＜t＜4）．

（1）连接DP，当t＞1时，四边形EQDP能够成为平行四边形吗？请说明理由；

（2）连接PQ，在运动过程中，不论t取何值，总有PQ与AB平行．为什么？

（3）当t为何值时，△EDQ为直角三角形？

Answer 1

【答案】（1）（2）见解析 （3）当t=2.5秒或t=3.1秒时，△EDQ为直角三角形．

【解析】（1）先根据点P以1厘米/秒的速度沿AC向终点C运动，点Q以1.25厘米/秒的速度沿BC向终点C运动求出1秒后AP及BQ的长，进而可得出QD及的长，再由PE∥BC可知，故可得出PE=QD，由PE∥BC即可得出结论；

（2）先用t表示出PC及CQ的长，再求出即可得出结论；

（3）分∠EQP=90°，∠QED=90°两种情况，通过三角形相似，列出比例关系，求出t的值即可．

解：（1）能，

如图1，

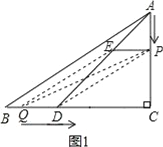
∵点P以1厘米/秒的速度沿AC向终点C运动，点Q以1.25厘米/秒的速度沿BC向终点C运动，t=1秒，

∴AP=1厘米，BQ=1.25厘米，

∵AC=4cm，BC=5cm，点D在BC上，CD=3cm，

∴PC=AC﹣AP=4﹣1=3（厘米），QD=BC﹣BQ﹣CD=5﹣1.25﹣3=0.75（厘米），

∵PE∥BC，

∴△APE∽△ACD，

∴,，解得PE=0.75，

∵PE∥BC，PE=QD，

∴四边形EQDP是平行四边形；

（2）如图2，

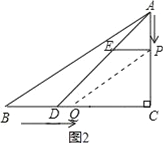
∵点P以1厘米/秒的速度沿AC向终点C运动，点Q以1.25厘米/秒的速度沿BC向终点C运动，

∴PC=AC﹣AP=4﹣t，QC=BC﹣BQ=5﹣1.25t，

∴，，

∴，

又∵∠C=∠C，

∴△CPQ∽△CAB，

∴∠CPQ=∠CAB，

∴PQ∥AB；

（3）分两种情况讨论：

①如图3，

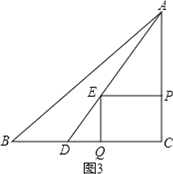
当∠EQD=90°时，显然有EQ=PC=4﹣t，

又∵EQ∥AC，

∴△EDQ∽△ADC

∴，

∵BC=5厘米，CD=3厘米，

∴BD=2厘米，

∴DQ=1.25t﹣2，

∴，解得t=2.5（秒）；

②如图4，

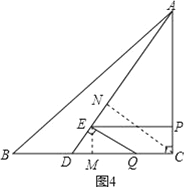
当∠QED=90°时，作EM⊥BC于M，CN⊥AD于N，则四边形EMCP是矩形，EM=PC=4﹣t，

在Rt△ACD中，

∵AC=4厘米，CD=3厘米，

∴AD==5，

∴CN=，

∵∠CDA=∠EDQ，∠QED=∠C=90°，

∴△EDQ∽△CDA，

∴，

∴，

解得t=3.1（秒）．

综上所述，当t=2.5秒或t=3.1秒时，△EDQ为直角三角形．

“点睛”此题是四边形纵综合题，主要考查了相似三角形的判定和性质，平行线的判定和性质，直角三角形的性质，解（1）的关键是判定出△APE∽△ACD，解（2）的关键是判断出，解（3）的关键是用分类讨论的思想解决问题．