
【题目】如图①,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE.
(2)如图②,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,AF=BF,原题设其他条件不变.求证:△AEF≌△BCF.
【答案】
(1)证明:∵AB=AC,D是BC的中点,∴∠BAE=∠CAE.
在△ABE和△ACE中, 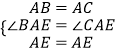 ∴△ABE≌△ACE(SAS).
∴△ABE≌△ACE(SAS).
∴BE=CE 。
(2)证明:∵AB=AC, 点D是BC的中点,
∴AD⊥BC.
∴∠EAF+∠C=90°.
∵BF⊥AC,
∴∠CBF+∠C=90°.
∴∠EAF=∠CBF.
在△AEF和△BCF中, 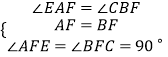
∴△AEF≌△BCF(ASA) 。
【解析】(1)根据等腰三角形的三线合一得出 :∠BAE=∠CAE,然后利用SAS判断出△ABE≌△ACE , 根据全等三角形对应边相等得出BE=CE ;
(2)根据等腰三角形的三线合一得出AD⊥BC,根据直角三角形两锐角互余得出∠EAF+∠C=90° , ∠CBF+∠C=90°,根据同角的余角相等得出∠EAF=∠CBF,然后根据ASA判断出△AEF≌△BCF 。
【考点精析】解答此题的关键在于理解余角和补角的特征的相关知识,掌握互余、互补是指两个角的数量关系,与两个角的位置无关,以及对等腰三角形的性质的理解,了解等腰三角形的两个底角相等(简称:等边对等角).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】小明、小刚和小红各自随机选择本周日的上午或下午去扬州科技馆参观.
(1) 小明、小刚本周日的上午去参观的概率为_____;
(2) 求他们三人在同一半天去参观的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.44°
B.66°
C.88°
D.92°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点B,C,E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )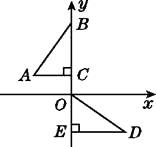
A.△ABC绕点C顺时针旋转90°,再向下平移3个单位长度
B.△ABC绕点C顺时针旋转90°,再向下平移1个单位长度
C.△ABC绕点C逆时针旋转90°,再向下平移1个单位长度
D.△ABC绕点C逆时针旋转90°,再向下平移3个单位长度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线C1:y=x2+4x﹣3与x轴交于A、B两点,将C1向右平移得到C2,C2与x轴交于B、C两点.
(1)求抛物线C2的解析式.
(2)点D是抛物线C2在x轴上方的图象上一点,求S△ABD的最大值.
(3)直线l过点A,且垂直于x轴,直线l沿x轴正方向向右平移的过程中,交C1于点E交C2于点F,当线段EF=5时,求点E的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com