
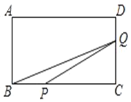
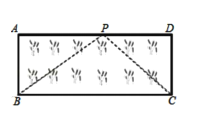
【题目】如图,已知矩形ABCD中,AB=4cm,BC=8cm.动点P在边BC上从点B向C运动,速度为1cm/s;同时动点Q从点C出发,沿折线C→D→A运动,速度为2cm/s.当一个点到达终点时,另一个点随之停止运动。设点P运动的时间为t(s),△BPQ的面积为S(cm2),则描述S(cm2)与时间t(s)的函数关系的图象大致是( )
A.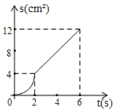 B.
B.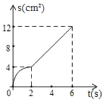
C.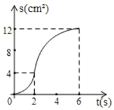 D.
D.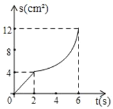
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
(1)求y与x的函数解析式;
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣![]() x2+bx+c与x轴交于点A(4,0),与y轴交于点B(0,4),在x轴上有一动点D9(m,0)(0<m<4),过点D作x轴的垂线交直线AB于点C,交抛物线于点E,
x2+bx+c与x轴交于点A(4,0),与y轴交于点B(0,4),在x轴上有一动点D9(m,0)(0<m<4),过点D作x轴的垂线交直线AB于点C,交抛物线于点E,
(1)直接写出抛物线和直线AB的函数表达式.
(2)当点C是DE的中点时,求出m的值,并判定四边形ODEB的形状(不要求证明).
(3)在(2)的条件下,将线段OD绕点O逆时针旋转得到OD′,旋转角为α(0°<a<90°),连接D′A、D′B,求D′A+![]() D′B的最小值.
D′B的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
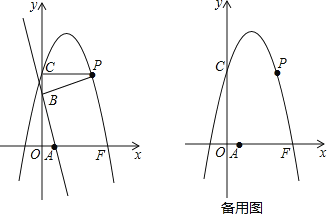
【题目】如图,直线y=﹣3x+3与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c与直线y=c分别交y轴的正半轴于点C和第一象限的点P,连接PB,得△PCB≌△BOA(O为坐标原点).若抛物线与x轴正半轴交点为点F,设M是点C,F间抛物线上的一点(包括端点),其横坐标为m.
(1)直接写出点P的坐标和抛物线的解析式;
(2)当m为何值时,△MAB面积S取得最小值和最大值?请说明理由;
(3)求满足∠MPO=∠POA的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+c和一次函数g(x)=﹣bx,其中a、b、c,满足a>b>c,a+b+c=0.
(1)求证:这两个函数的图象交于不同的两点;
(2)设这两个函数的图象交于A,B两点,作AA1⊥x轴于A1,BB1⊥x轴于B1,求线段A1B1的长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC于点D,交BC于点E,连接ED.
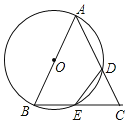
(1)求证:ED=EC;
(2)填空:
①设CD的中点为P,连接EP,则EP与⊙O的位置关系是 ;
②连接OD,当∠B的度数为 时,四边OBED是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC和△EFC中,∠ABC=∠EFC=90°,点E在△ABC内,且∠CAE+∠CBE=90°
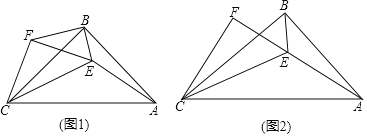
(1)如图1,当△ABC和△EFC均为等腰直角三角形时,连接BF,
①求证:△CAE∽△CBF;
②若BE=2,AE=4,求EF的长;
(2)如图2,当△ABC和△EFC均为一般直角三角形时,若![]() =k,BE=1,AE=3,CE=4,求k的值.
=k,BE=1,AE=3,CE=4,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元二次方程,把它转化为两个一元一次方程来解,求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验,各类方程的解法不尽相同,但是它们有一个共同的基本数学思想“转化”,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.
例如:解方程![]()
解:移项,得![]()
两边平方,得![]()
即![]()
两边再平方,得![]()
即![]()
解这个方程得:![]()
检验:当![]() 时,原方程左边
时,原方程左边![]() ,右边
,右边![]()
![]() 不是原方程的根;
不是原方程的根;
当![]() 时,原方程左边
时,原方程左边![]() ,右边
,右边![]()
![]() 原方程的根
原方程的根
![]() 原方程的根是
原方程的根是![]() .
.
(1)请仿照上述解法,求出方程![]() 的解;
的解;
(2)如图已知矩形草坪![]() 的长
的长![]() ,宽
,宽![]() ,小华把一根长为
,小华把一根长为![]() 的绳子的一端固定在点
的绳子的一端固定在点![]() ,从草坪边沿
,从草坪边沿![]() 走到点
走到点![]() 处,把长绳
处,把长绳![]() 段拉直并固定在点
段拉直并固定在点![]() ,然后沿草坪边沿
,然后沿草坪边沿![]() 走到点
走到点![]() 处,把长绳剩下的一段拉直,长绳的另一端恰好落在点
处,把长绳剩下的一段拉直,长绳的另一端恰好落在点![]() ,则
,则![]()
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com