
����Ŀ������ABCD�У������Խ���AC��BD�ཻ�ڵ�O����MON+��BCD=180�㣬��MON�Ƶ�O��ת������OM����BC�ڵ�E������ON����DC�ڵ�F������EF��
��1����ͼ1������ABC=90��ʱ����OEF����״����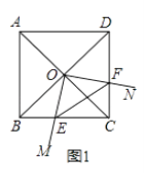
��2����ͼ2������ABC=60��ʱ�����жϡ�OEF����״����˵�����ɣ�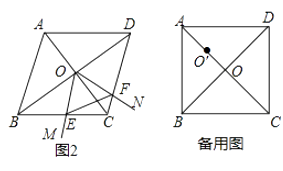
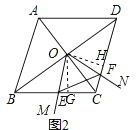
��3���ڣ�1���������£�����MON�Ķ����Ƶ�AO���е�O�䴦����MO��N�Ƶ�O����ת���������MO��N+��BCD=180�㣬����O��M��ֱ��BC�ڵ�E������O��N��ֱ��CD�ڵ�F����BC=4���� ![]() =
= ![]() ʱ��ֱ��д���߶�CE�ij���
ʱ��ֱ��д���߶�CE�ij���
���𰸡�
��1������ֱ��������
��2����OEF�ǵȱ������Σ�
֤������ͼ2����O����OG��BC��G����OH��CD��H��
���OGE=��OGC=��OHC=90�㣬
���ı���ABCD�����Σ�
��CAƽ�֡�BCD����ABC+BCD=180�㣬
��OG=OH����BCD=180�㩁60��=120�㣬
�ߡ�GOH+��OGC+��BCD+��OHC=360�㣬
���GOH+��BCD=180�㣬
���MON+��BCD=180�㣬
���GOH=��EOF=60�㣬
�ߡ�GOH=��GOF+��FOH����EOF=��GOF+��EOG��
���EOG=��FOH��
�ڡ�EOG���FOH�У�
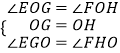 ��
��
���EOG�ա�FOH��ASA����
��OE=OF��
���OEF�ǵȱ�������
��3��֤������ͼ3��
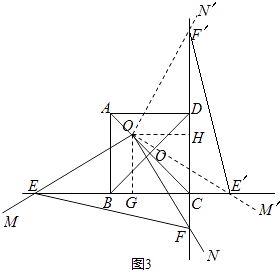
������ABCD�У���ABC=90�㣬
���ı���ABCD�������Σ�
�� ![]() =
= ![]() ��
��
��O����O��G��BC��G����O��H��CD��H��
���O��GC=��O��HC=��BCD=90�㣬
���ı���O��GCH�Ǿ��Σ�
��O��G��AB��O��H��AD��
�� ![]() =
= ![]() =
= ![]() =
= ![]() ��
��
��AB=BC=CD=AD=4��
��O��G=O��H=3��
���ı���O��GCH�������Σ�
��GC=O��G=3����GO��H=90��
�ߡ�MO��N+��BCD=180�㣬
���EO��F=90�㣬
���EO��F=��GO��H=90�㣬
�ߡ�GO��H=��GO��F+��FO��H����EO��F=��GO��F+��EO��G��
���EO��G=��FO��H��
�ڡ�EO��G���FO��H�У�
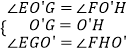 ��
��
���EO��G�ա�FO��H��ASA����
��O��E=O��F��
���O��EF�ǵ���ֱ�������Σ�
��S������ABCD=4��4=16�� ![]() =
= ![]() ��
��
��S��O��EF=18��
��S��O��EF= ![]() O��E2��
O��E2��
��O��E=6��
��RT��O��EG��EG= ![]() =
= ![]() =3
=3 ![]() ��
��
��CE=CG+EG=3+3 ![]() ��
��
���ݶԳ��Կ�֪������M��ON����ת����ͼ��ʾλ��ʱ��
CE��=E��G��CG=3 ![]() ��3��
��3��
���Ͽɵã��߶�CE�ij�Ϊ3+3 ![]() ��3
��3 ![]() ��3��
��3��
����������1����OEF�ǵ���ֱ�������Σ�
֤������ͼ1��
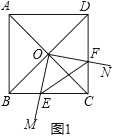
������ABCD�У���ABC=90�㣬
���ı���ABCD�������Σ�
��OB=OC����BOC=90�㣬��BCD=90�㣬��EBO=��FCO=45�㣬
���BOE+��COE=90�㣬
�ߡ�MON+��BCD=180�㣬
���MON=90�㣬
���COF+��COE=90�㣬
���BOE=��COF��
�ڡ�BOE���COF�У�
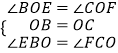 ��
��
���BOE�ա�COF��ASA����
��OE=OF��
���OEF�ǵ���ֱ�������Σ�
��2����OEF�ǵȱ������Σ�
֤������ͼ2����O����OG��BC��G����OH��CD��H��

���OGE=��OGC=��OHC=90�㣬
���ı���ABCD�����Σ�
��CAƽ�֡�BCD����ABC+BCD=180�㣬
��OG=OH����BCD=180�㩁60��=120�㣬
�ߡ�GOH+��OGC+��BCD+��OHC=360�㣬
���GOH+��BCD=180�㣬
���MON+��BCD=180�㣬
���GOH=��EOF=60�㣬
�ߡ�GOH=��GOF+��FOH����EOF=��GOF+��EOG��
���EOG=��FOH��
�ڡ�EOG���FOH�У�
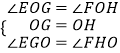 ��
��
���EOG�ա�FOH��ASA����
��OE=OF��
���OEF�ǵȱ�������
��3��֤������ͼ3��

������ABCD�У���ABC=90�㣬
���ı���ABCD�������Σ�
�� ![]() =
= ![]() ��
��
��O����O��G��BC��G����O��H��CD��H��
���O��GC=��O��HC=��BCD=90�㣬
���ı���O��GCH�Ǿ��Σ�
��O��G��AB��O��H��AD��
�� ![]() =
= ![]() =
= ![]() =
= ![]() ��
��
��AB=BC=CD=AD=4��
��O��G=O��H=3��
���ı���O��GCH�������Σ�
��GC=O��G=3����GO��H=90��
�ߡ�MO��N+��BCD=180�㣬
���EO��F=90�㣬
���EO��F=��GO��H=90�㣬
�ߡ�GO��H=��GO��F+��FO��H����EO��F=��GO��F+��EO��G��
���EO��G=��FO��H��
�ڡ�EO��G���FO��H�У�
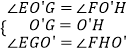 ��
��
���EO��G�ա�FO��H��ASA����
��O��E=O��F��
���O��EF�ǵ���ֱ�������Σ�
��S������ABCD=4��4=16�� ![]() =
= ![]() ��
��
��S��O��EF=18��
��S��O��EF= ![]() O��E2��
O��E2��
��O��E=6��
��RT��O��EG��EG= ![]() =
= ![]() =3
=3 ![]() ��
��
��CE=CG+EG=3+3 ![]() ��
��
���ݶԳ��Կ�֪������M��ON����ת����ͼ��ʾλ��ʱ��
CE��=E��G��CG=3 ![]() ��3��
��3��
���Ͽɵã��߶�CE�ij�Ϊ3+3 ![]() ��3
��3 ![]() ��3��
��3��
���Դ��ǣ���1������ֱ�������Σ���2���������̣���3��3+3 ![]() ��3
��3 ![]() ��3��
��3��


 ������ȫ��������ϵ�д�
������ȫ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ԲO��Rt��ABC�����Բ����ACB=90�㣬��A=25�㣬����C��ԲO�����ߣ���AB���ӳ����ڵ�D�����D�Ķ����ǣ� �� 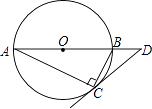
A.25��
B.40��
C.50��
D.65��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��¥�Ķ�������һ������CD��С����ɽ�µ��½�A����ù���Ƶ�����Ϊ60�㣬���¶�Ϊ1�� ![]() ������AB�������ߵ�B������ù���ƶ���C������Ϊ45�㣬��֪AB=10m��AE=15m��������CD�ĸ߶ȣ���ȷ��0.1m������ǵĸ߶Ⱥ��Բ��ƣ�
������AB�������ߵ�B������ù���ƶ���C������Ϊ45�㣬��֪AB=10m��AE=15m��������CD�ĸ߶ȣ���ȷ��0.1m������ǵĸ߶Ⱥ��Բ��ƣ�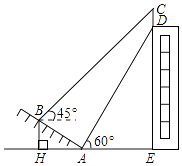
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֤��:
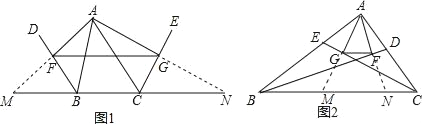
��1����֪����ͼ1��BD��CE�ֱ��ǡ�ABC�����ƽ���ߣ�����A��AF��BD��AG��CE������ֱ���F��G������FG���ӳ�AF��AG����ֱ��BC�ཻ����֤��FG��![]() ��AB+BC+AC����
��AB+BC+AC����
��2����BD��CE�ֱ��ǡ�ABC���ڽ�ƽ���ߣ������������䣨��ͼ1�����߶�FG���ABC����������������������ϵ��д����IJ��룬������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2008����˻��ڼ䣬һ����ͳ���һ���ϱ�����ĵ�·�����������ÿͣ�ijһ���糿�ó���A�س��������ϵ���B�أ�Ԥ����Ϊ����������ʻ��¼����(��λ��ǧ��)
+18��-9��+7��-14��-6��+13��-6��-8
������ݼ���ش��������⣺
��1��B����A�غη���������ǧ�ף�
��2���ó���һ�칲��ʻ����ǧ�ף�
��3�����ó�ÿǧ����0.4������һ�칲���Ͷ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������L��y=�� ![]() ��x+t����x��t+4����x��ֻ��һ�����㣬��������L��x��Ľ��������� ��
��x+t����x��t+4����x��ֻ��һ�����㣬��������L��x��Ľ��������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽�ȫУ2000��ѧ��ÿ��ȥͼ���ʱ��������������������е�100��ѧ��������100��ѧ��ÿ��ȥͼ��ݵ�ʱ��x����λ��Сʱ��������ͳ�ƣ������������ݻ�����һ����������ͳ��ͼ����֪��ÿ��ȥͼ��ݵ�ʱ����6��x��8Сʱ��ѧ������ռ20%������������Ϣ��ͳ��ͼ����������⣺ 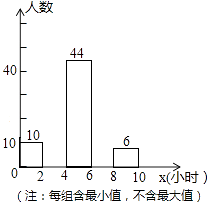
��1�����ε����������飬������������
��2���벹ȫƵ���ֲ�ֱ��ͼ�п�ȱ�IJ��֣�
��3��������100��ѧ���������ȡ1��ѧ�������ȡ�����ѧ��ÿ��ȥͼ��ݵ�ʱ��ǡ����8��10Сʱ�ĸ��ʣ�
��4������ȫУѧ��ÿ��ȥͼ��ݵ�ʱ�䲻����6Сʱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A�������϶�Ӧ����Ϊa����B�������϶�Ӧ����Ϊb����|a+3|+|b-2|=0��A,B ֮��ľ����Ϊ|AB|.��ش����⣺
(1)ֱ��д��a,b, |AB|��ֵ. a= ��b = �� |AB|= ��
(2)���P�������϶�Ӧ����Ϊx����|PA|-|PB|=2ʱ����x��ֵ��
(3)����P�ڵ�A����࣬M��N�ֱ���PA��PB���е�.����P�ڵ�A������ƶ�ʱ��ʽ��|PN|-|PM|��ֵ�Ƿ����ı䣿�����䣬�������ֵ���������仯����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����λͬѧ��һ��ʵ����ͳ����ijһ������ֵ�Ƶ�ʣ�������ͳ��ͼ��ͼ��ʾ���� ������һ�����ʵ������ǣ� ��

A. ��һö������������ӣ�����6��ĸ���
B. ��һöӲ�ң��������泯�ϵĸ���
C. ����д��һ���������ܱ�2�����ĸ���
D. һ��������װ��ֻ����ɫ��ͬ����������ͬ�����������һ������������ȡ��һ���ǻ���ĸ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com