
����Ŀ����ƽ��ֱ�������У��ı���OCNMΪ���Σ���ͼ1��M������Ϊ��m��0����C������Ϊ��0��n������֪m��n����![]() ��
��
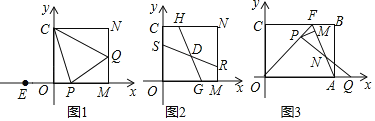
��1����m��n��ֵ��
��2������ͼ1��P��Q�ֱ�ΪOM��MN��һ�㣬����PCQ��45������֤��PQ��OP+NQ��
����ͼ2��S��G��R��H�ֱ�ΪOC��OM��MN��NC��һ�㣬SR��HG���ڵ�D������SDG��135����![]() ����RS��______��
����RS��______��
��3����ͼ3���ھ���OABC�У�OA��5��OC��3����F�ڱ�BC����OF��OA������AF������P���߶�OF�ǣ�����P��O��F���غϣ�������Q���߶�OA���ӳ����ϣ���AQ��FP������PQ��AF�ڵ�N����PM��AF��M�����ʣ���P��Q���ƶ������У��߶�MN�ij����Ƿ����仯������������߶�MN�ij��ȣ����仯����˵�����ɣ�
���𰸡���1��m��5��n=5����2����֤������������![]() ����3��MN�ij��Ȳ��ᷢ���仯�����ij���Ϊ
����3��MN�ij��Ȳ��ᷢ���仯�����ij���Ϊ![]() ��
��
��������
��1�����÷Ǹ��������ʼ��ɽ�����⣮
��2�����������ߣ���������������ȫ�ȣ�֤����COE�ա�CNQ����ECP�ա�QCP����PE��PQ��OE+OP���ó����ۣ�
���������ߣ�����ƽ���ı��κ�ȫ�������Σ��ɵ�CSRE��CFGH����CE��SR��CF��GH��֤����CEN�ա�CE��O����E��CF�ա�ECF����EF��E��F����EN��x����Rt��MEF�У����ݹ��ɶ����з������EN�ij��������ù��ɶ�����CE����SR��CE��ȣ�����SR��![]() ��
��
��3���ڣ�1���������£���P��Q���ƶ��������߶�MN�ij��Ȳ��ᷢ���仯�����MN�ij����ɣ���ͼ4����P��PD��OQ��֤����PDF�ǵ��������Σ������ߺ�һ�ã�DM��![]() FD��֤����PND�ա�QNA����DN��
FD��֤����PND�ա�QNA����DN��![]() AD����MN��
AD����MN��![]() AF�����AF�ij����ɽ�����⣮
AF�����AF�ij����ɽ�����⣮
�⣺��1����![]() ��
��
����![]() ��0��|5��m|��0��
��0��|5��m|��0��
��n��5��0��5��m��0��
��m��5��n=5��
��2������ͼ1�У���PO���ӳ�����ȡһ��E��ʹNQ��OE��
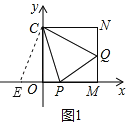
��CN��OM��OC��MN����COM��90����
���ı���OMNC�������Σ�
��CO��CN��
�ߡ�EOC����N��90����
���COE�ա�CNQ��SAS����
��CQ��CE����ECO����QCN��
�ߡ�PCQ��45����
���QCN+��OCP��90����45����45����
���ECP����ECO+��OCP��45����
���ECP����PCQ��
��CP��CP��
���ECP�ա�QCP��SAS����
��EP��PQ��
��EP��EO+OP��NQ+OP��
��PQ��OP+NQ��
����ͼ2�У���C��CE��SR����x�Ḻ������ȡһ��E����ʹOE����EN����CSRE������CEN�ա�CE��O����CE��SR��
��C��CF��GH��OM��F������FE����CFGH����CF��GH��![]() ��
��

�ߡ�SDG��135����
���SDH��180����135����45����
���FCE����SDH��45����
���NCE+��OCF��
�ߡ�CEN�ա�CE��O��
���E��CO����ECN��CE��CE����
���E��CF����E��CO+��OCF��45����
���E��CF����FCE��
��CF��CF��
���E��CF�ա�ECF��SAS����
��E��F��EF
��Rt��COF��OC��5��FC��![]() ��
��
�ɹ��ɶ����ã�OF�� ��
��![]() ��
��
��FM��5��![]() ��
��![]() ��
��
��EN��x����EM��5��x��FE��E��F��x+![]() ��
��
��x+![]() ��2����
��2����![]() ��2+��5��x��2��
��2+��5��x��2��
��ã�x��![]() ��
��
��EN��![]() ��
��
�ɹ��ɶ����ã�CE��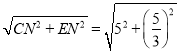 ��
��![]() ��
��
��SR��CE��![]() ��
��
�ʴ�Ϊ![]() ��
��
��3����P��Q���ƶ��������߶�MN�ij��Ȳ��ᷢ���仯��
���ɣ���ͼ3�У���P��PD��OQ����AF��D��
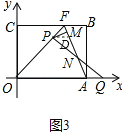
��OF��OA��
���OFA����OAF����PDF��
��PF��PD��
��PF��AQ��
��PD��AQ��
��PM��AF��
��DM��![]() FD��
FD��
��PD��OQ��
���DPN����PQA��
�ߡ�PND����QNA��
���PND�ա�QNA��AAS����
��DN��AN��
��DN��![]() AD��
AD��
��MN��DM+DN��![]() DF+
DF+![]() AD��
AD��![]() AF��
AF��
��OF��OA��5��OC��3��
��CF��![]() ��
��
��BF��BC��CF��5��4��1��
��AF��![]() ��
��
��MN��![]() AF��
AF��![]() ��
��
����P��Q���ƶ��������߶�MN�ij��Ȳ��ᷢ���仯�����ij���Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������:
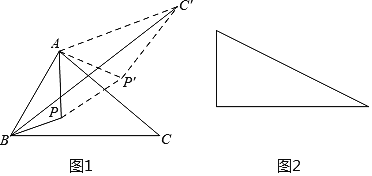
�����P�������ABC��һ���㣬���ȷ��һ��λ�ã�ʹ��P����ABC��������ľ���֮��PA+PB+PC��ֵΪ��С?
�����ת��:
(1)����APC�Ƶ�A��ʱ����ת60�ȵõ�![]() ����
����![]() �����Ͱ�ȷ��PA+PB+PC����Сֵ������ת����ȷ��
�����Ͱ�ȷ��PA+PB+PC����Сֵ������ת����ȷ��![]() ����Сֵ��������,����������ͼ֤��:
����Сֵ��������,����������ͼ֤��:
![]() ��
��
����Ľ��:
(2)����P�������ABC�������ľ���֮��PA+PB+PC��ֵΪ��Сʱ��������һ����������ϵ�̻���ʱ�ĵ�P��λ��:_____________________________��
��������죺
(3)��ͼ����һ�����Ϊ30����ֱ�������Σ����б��Ϊ2����P�������������һ���㣬�����������Ϸ��������P����������θ�����ľ���֮�͵���Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
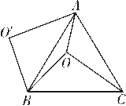
����Ŀ����ͼ��O�ǵȱߡ�ABC��һ�㣬OA=3��OB=4��OC=5�����߶�BO�Ե�BΪ��ת������ʱ����ת60��õ��߶�BO�䣬���н��ۣ�
�١�BO��A�����ɡ�BOC�Ƶ�B��ʱ����ת60��õ���&
�ڵ�O��O��ľ���Ϊ4��
�ۡ�AOB=150�㣻
���ı���AOBO������Ϊ6��3![]() ��
��
��S��AOC��S��AOB=6��![]() .
.
������ȷ�Ľ�����_______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������־Ը�߰���С�ֶӸ�ɽ������ů����Ϊ���Ѵ�����һЩ����.��֪����1�����ס�4����ۣ�����240Ԫ������2�����ס�1����ۣ�����165Ԫ.
��1����ÿ��������۸�����Ԫ��
��2���������С�ֶӼƻ�������Щ���湲40�����ܷ��ò�����2140Ԫ����ô���ٹ�����ٴ����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
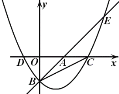
����Ŀ����ͼ��ֱ��y=x-3�������ύ��A��B���㣬������![]() ������B����ֱ��y=x-3���ڵ�E��8��5��������x�ύ��C��D����.
������B����ֱ��y=x-3���ڵ�E��8��5��������x�ύ��C��D����.
��1���������ߵĽ���ʽ��
��2������������һ��M������MBE=75��ʱ�����M�ĺ����ꣻ
��3����P���������ϣ�������ƽ�����Ƿ���ڵ�Q��ʹ���Ե�P��Q��B��CΪ������ı����Ǿ��Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ж� 600 ����ҵ���п�����������λ��ǰ���ɼ��������������Ƴ� ���²�������ͳ��ͼ��
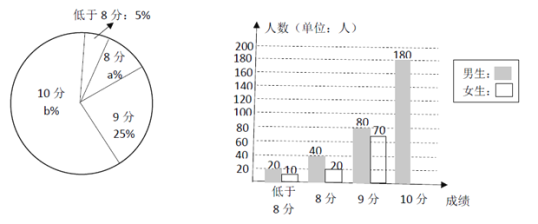
����ͳ��ͼ���ش��������⡣
(1)�뽫����ͳ��ͼ����������
(2)����ͳ��ͼ�У�b= ���� 8 ������Ӧ���ε�Բ�ĽǶ���Ϊ ;
(3)�ڱ��ε����ѧ���У������ȡ 1 �����������ijɼ������� 9 �ֵĸ���Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
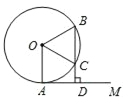
����Ŀ����ͼ��AMΪ��O�����ߣ�AΪ�е㣬����O��һ��B��BD��AM�ڵ�D��BD����O��C��OCƽ�֡�AOB��
��1�����AOB�Ķ�����
��2�����߶�CD�ij�Ϊ2cm����![]() �ij��ȣ�
�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���![]() ��
��
��1����֤����һԪ���η�����������ʵ������
��2�����÷���ֻ��һ��С��4�ĸ�����m��ȡֵ��Χ��
��3����x1��x2Ϊ���̵�����������n��x12+x22��4���ж϶���![]() ���γɵ���ͼ���Ƿ���
���γɵ���ͼ���Ƿ���![]() ����˵�����ɣ�
����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ĺ�������5��С�ֱ�������֩�3����2����1����![]() ����
����![]() ����ЩС������������ͬ�������ͬ���ȴӺ����������1����������������ٴ�ʣ�µ������������1���������������
����ЩС������������ͬ�������ͬ���ȴӺ����������1����������������ٴ�ʣ�µ������������1���������������
��1���û���״ͼ���б��ķ������������������������֮��������1�ĸ��ʣ�
��2�����Ե�һ���������ϵ�����Ϊ�����꣬�ڶ����������ϵ�����Ϊ������ȷ��һ�㣬ֱ��д���õ���˫����y=![]() �ϵĸ��ʣ�
�ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com