
【题目】问题的提出:
如果点P是锐角△ABC内一动点,如何确定一个位置,使点P到△ABC的三顶点的距离之和PA+PB+PC的值为最小?
问题的转化:
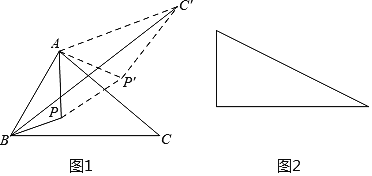
(1)把ΔAPC绕点A逆时针旋转60度得到![]() 连接
连接![]() 这样就把确定PA+PB+PC的最小值的问题转化成确定
这样就把确定PA+PB+PC的最小值的问题转化成确定![]() 的最小值的问题了,请你利用如图证明:
的最小值的问题了,请你利用如图证明:
![]() ;
;
问题的解决:
(2)当点P到锐角△ABC的三项点的距离之和PA+PB+PC的值为最小时,请你用一定的数量关系刻画此时的点P的位置:_____________________________;
问题的延伸:
(3)如图是有一个锐角为30°的直角三角形,如果斜边为2,点P是这个三角形内一动点,请你利用以上方法,求点P到这个三角形各顶点的距离之和的最小值.
【答案】(1)证明见解析;(2)∠APB=∠APC=120°;(3)![]() .
.
【解析】
(1)问题的转化:
根据旋转的性质证明△APP'是等边三角形,则PP'=PA,可得结论;
(2)问题的解决:
运用类比的思想,把△APC绕点A逆时针旋转60度得到△AP′C′,连接PP′,由“问题的转化”可知:当B、P、P'、C'在同一直线上时,PA+PB+PC的值为最小,确定当:∠APB=∠APC=120°时,满足三点共线;
(3)问题的延伸:
如图3,作辅助线,构建直角△ABC',利用勾股定理求AC'的长,即是点P到这个三角形各顶点的距离之和的最小值.
问题的转化:
如图1,
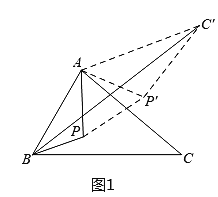
由旋转得:∠PAP'=60°,PA=P'A,
∴△APP'是等边三角形,
∴PP'=PA,
∵PC=P'C,
∴PA+PB+PC=BP+PP′+P′C′.
问题的解决:
满足:∠APB=∠APC=120°时,PA+PB+PC的值为最小;
理由是:如图2,把△APC绕点A逆时针旋转60度得到△AP′C′,连接PP′,
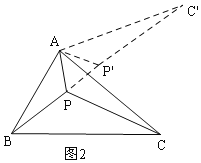
由“问题的转化”可知:当B、P、P'、C'在同一直线上时,PA+PB+PC的值为最小,
∵∠APB=120°,∠APP'=60°,
∴∠APB+∠APP'=180°,
∴B、P、P'在同一直线上,
由旋转得:∠AP'C'=∠APC=120°,
∵∠AP'P=60°,
∴∠AP'C'+∠AP'P=180°,
∴P、P'、C'在同一直线上,
∴B、P、P'、C'在同一直线上,
∴此时PA+PB+PC的值为最小,
故答案为∠APB=∠APC=120°;
问题的延伸:
如图3,
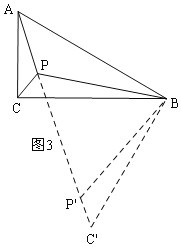
Rt△ACB中,∵AB=2,∠ABC=30°,
∴AC=1,BC=![]() ,
,
把△BPC绕点B逆时针旋转60度得到△BP′C′,连接PP′,
当A、P、P'、C'在同一直线上时,PA+PB+PC的值为最小,
由旋转得:BP=BP',∠PBP'=60°,PC=P'C',BC=BC',
∴△BPP′是等边三角形,
∴PP'=PB,
∵∠ABC=∠APB+∠CBP=∠APB+∠C'BP'=30°,
∴∠ABC'=90°,
由勾股定理得:AC'=![]() ,
,
∴PA+PB+PC=PA+PP'+P'C'=AC'=![]() ,
,
则点P到这个三角形各顶点的距离之和的最小值为![]() .
.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】某种电子产品共4件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为![]() .
.
(1)该批产品有正品________件;
(2)如果从中任意取出2件,利用列表或树状图求取出2件都是正品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组![]() .
.
(1)当m=2时,请解关于x、y的方程组![]() ;
;
(2)若关于x、y的方程组![]() 中,x为非负数、y为负数,
中,x为非负数、y为负数,
①试求m的取值范围;
②当m取何整数时,不等式3mx+2x>3m+2的解为x<1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着地面公交和共享单车的发展,“公交车+单车”的方式已成为很多市民出行的选择。小明放学后从寿春中学出发,先乘坐公交车,根据路面交通的拥堵的实际情况,灵活决定在离家较近的A、B、C、D、E中的某一公交站下车,再骑共享单车回家,设他乘公交车的时间y1(单位:分钟)与下车站点到学校距离x(3≤x≤5)(单位:千米)之间函数关系为y1=2x+2,小明骑单车的时间y2(单位:分钟)与x(3≤x≤5)之间的满足二次函数关系,其具体对应值如下表所示:
地铁站 | A | B | C | D | E |
X(千米) | 3 |
| 4 |
| 5 |
Y2(分钟) | 11 |
| 6 |
| 3 |
(1)求y2关于x的函数表达式;
(2)求小明从学校回到家的时间y(单位:分钟)与x的函数表达式;
(3)请通过计算说明:小明应选择在哪一站下公交车,才能使他从学校回家所需的时间最短?并求出最短时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中装有3个白球、5个红球,这些球除了颜色外完全相同,充分摇匀后随机摸出一球,
(1)求摸出白球概率是多少?
(2)在第一次摸出白球后,如果将这个白球放回,再摸出一球,求两次摸出的都是白球的概率是多少?(用树状图或列表分析)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
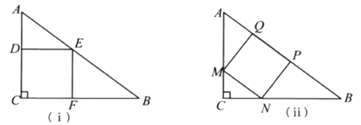
【题目】一块直角三角形的木板,它的一条直角边AC长为1.5米,面积为1.5平方米.现在要把它加工成一个正方形桌面,甲、乙两人的加工方法分别如图(ⅰ)、(ⅱ)所示,记两个正方形面积分别为S1、S2,请通过计算比较S1与S2的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com