
【题目】如图,直线OC、BC的函数关系式分别是y1=x和y2=﹣2x+6,直线BC与x轴交于点B,直线BA与直线OC相交于点A.
(1)当x取何值时y1>y2?
(2)当直线BA平分△BOC的面积时,求点A的坐标.

 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数y1=﹣2x﹣3与y2=![]() x+2.
x+2.
(1)在同一平面直角坐标系中,画出这两个函数的图象;
(2)根据图象,不等式﹣2x﹣3>![]() x+2的解集为多少?
x+2的解集为多少?
(3)求两图象和y轴围成的三角形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E为CD上一点,DE:EC=2:3,连接AE,BE,BD,且AE,BD交于点F,则S△DEF:S△EBF:S△ABF= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=60°.
(1)如图1,点E为线段AB的中点,连接DE,CE,若AB=4,求线段EC的长;
(2)如图2,M为线段AC上一点(M不与A,C重合),以AM为边,构造如图所示等边三角形AMN,线段MN与AD交于点G,连接NC,DM,Q为线段NC的中点,连接DQ,MQ,求证:DM=2DQ.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为了了解2013年初中毕业生毕业后的去向,对部分初三学生进行了抽样调查,就初三学生的四种去向
A.读普通高中; | B.读职业高中 | C.直接进入社会就业; | D.其它)进行数据统计,并绘制了两幅不完整的统计图(a)、(b).请问: |


(1)该县共调查了 名初中毕业生;
(2)将两幅统计图中不完整的部分补充完整;
(3)若该县2013年初三毕业生共有4500人,请估计该县今年的初三毕业生中读普通高中的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣ ![]() x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A,B两点.
x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A,B两点.
(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的一点,连接PA、PB、PO,若△POA的面积是△POB面积的 ![]() 倍.
倍.
①求点P的坐标;
②点Q为抛物线对称轴上一点,请直接写出QP+QA的最小值;
(3)点M为直线AB上的动点,点N为抛物线上的动点,当以点O、B、M、N为顶点的四边形是平行四边形时,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,有若干个点按如下规律排列:(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),…, 则第 200 个点的横坐标为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y= ![]() x2﹣2x+1的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.
x2﹣2x+1的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.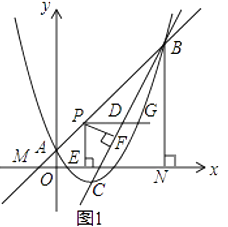
(1)求直线AB和直线BC的解析式;
(2)点P是线段AB上一点,点D是线段BC上一点,PD∥x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F.当PF与PE的乘积最大时,在线段AB上找一点H(不与点A,点B重合),使GH+ ![]() BH的值最小,求点H的坐标和GH+
BH的值最小,求点H的坐标和GH+ ![]() BH的最小值;
BH的最小值;
(3)如图2,直线AB上有一点K(3,4),将二次函数y= ![]() x2﹣2x+1沿直线BC平移,平移的距离是t(t≥0),平移后抛物线上点A,点C的对应点分别为点A′,点C′;当△A′C′K是直角三角形时,求t的值.
x2﹣2x+1沿直线BC平移,平移的距离是t(t≥0),平移后抛物线上点A,点C的对应点分别为点A′,点C′;当△A′C′K是直角三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为创建“美丽乡村”,某村计划购买甲、乙两种树苗共400棵,对本村道路进行绿化改造,已知甲种树苗每棵200元,乙种树苗每棵300元.
![]() 若购买两种树苗的总金额为90000元,求需购买甲、乙两种树苗各多少棵?
若购买两种树苗的总金额为90000元,求需购买甲、乙两种树苗各多少棵?
![]() 若购买甲种树苗的金额不少于购买乙种树苗的金额,则至少应购买甲种树苗多少棵?
若购买甲种树苗的金额不少于购买乙种树苗的金额,则至少应购买甲种树苗多少棵?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com