
【题目】在菱形ABCD中,∠BAD=60°.
(1)如图1,点E为线段AB的中点,连接DE,CE,若AB=4,求线段EC的长;
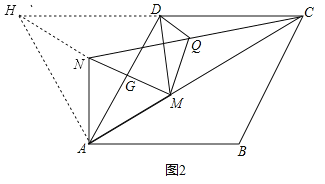
(2)如图2,M为线段AC上一点(M不与A,C重合),以AM为边,构造如图所示等边三角形AMN,线段MN与AD交于点G,连接NC,DM,Q为线段NC的中点,连接DQ,MQ,求证:DM=2DQ.

【答案】(1)2![]() (2)证明见解析
(2)证明见解析
【解析】试题分析:(1)如图1,连接对角线BD,先证明△ABD是等边三角形,根据E是AB的中点,由等腰三角形三线合一得:DE⊥AB,利用勾股定理依次求DE和EC的长;
(2)如图2,作辅助线,构建全等三角形,先证明△ADH是等边三角形,再由△AMN是等边三角形,得条件证明△ANH≌△AMD(SAS),则HN=DM,根据DQ是△CHN的中位线,得HN=2DQ,由等量代换可得结论.
试题解析:解:(1)如图1,连接BD,则BD平分∠ABC,∵四边形ABCD是菱形,∴AD∥BC,∴∠A+∠ABC=180°,∵∠A=60°,∴∠ABC=120°,∴∠ABD=![]() ∠ABC=60°,∴△ABD是等边三角形,∴BD=AD=4,∵E是AB的中点,∴DE⊥AB,由勾股定理得:DE=
∠ABC=60°,∴△ABD是等边三角形,∴BD=AD=4,∵E是AB的中点,∴DE⊥AB,由勾股定理得:DE=![]() =
=![]() ,∵DC∥AB,∴∠EDC=∠DEA=90°,在Rt△DEC中,DC=4,EC=
,∵DC∥AB,∴∠EDC=∠DEA=90°,在Rt△DEC中,DC=4,EC=![]() =
=![]() =
=![]() ;
;

(2)如图2,延长CD至H,使CD=DH,连接NH、AH,∵AD=CD,∴AD=DH,∵CD∥AB,∴∠HDA=∠BAD=60°,∴△ADH是等边三角形,∴AH=AD,∠HAD=60°,∵△AMN是等边三角形,∴AM=AN,∠NAM=60°,∴∠HAN+∠NAG=∠NAG+∠DAM,∴∠HAN=∠DAM,在△ANH和△AMD中,∵AH=AD,∠HAN=∠DAM,AN=AM,∴△ANH≌△AMD(SAS),∴HN=DM,∵D是CH的中点,Q是NC的中点,∴DQ是△CHN的中位线,∴HN=2DQ,∴DM=2DQ.


科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠3,CD∥EF,试说明∠1=∠4.请将过程填写完整.

解:∵∠1=∠3,
又∠2=∠3(_______),
∴∠1=____,
∴______∥______(_______),
又∵CD∥EF,
∴AB∥_____,
∴∠1=∠4(两直线平行,同位角相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,![]() ,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.若△BCD是等腰三角形,则四边形BDFC的面积为_______________。
,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.若△BCD是等腰三角形,则四边形BDFC的面积为_______________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抗击新冠病毒,保护学生和教师的生命安全,新希望中学![]() 元购进甲、乙两种医用口罩共计
元购进甲、乙两种医用口罩共计![]() 盒,甲,乙两种口罩的售价分别是
盒,甲,乙两种口罩的售价分别是![]() 元/盒,
元/盒,![]() 元/盒;甲,乙两 种口罩的数量分别是
元/盒;甲,乙两 种口罩的数量分别是![]() 个/盒,
个/盒,![]() 个/盒.
个/盒.
(1)求新希望中学甲、乙两种口罩各购进了多少盒?
(2)按照教育局要求,学校必须储备两周的用量,新希望中学师生共计![]() 人,每人每天
人,每人每天![]() 个口罩,问购买的口罩数量是否能满足教育局的要求?
个口罩,问购买的口罩数量是否能满足教育局的要求?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0),

(1)请直接写出点A关于原点O对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,求出A′点的坐标。
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延长CA到O,使AO=AC,以O为圆心,OA长为半径作⊙O交BA延长线于点D,连接CD.
(1)求证:CD是⊙O的切线;
(2)若AB=4,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线OC、BC的函数关系式分别是y1=x和y2=﹣2x+6,直线BC与x轴交于点B,直线BA与直线OC相交于点A.
(1)当x取何值时y1>y2?
(2)当直线BA平分△BOC的面积时,求点A的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距72千米,李磊骑自行车往返两地一共用了7小时,已知他去时的平均速度比返回时的平均速度快![]() ,求李磊去时的平均速度是多少?
,求李磊去时的平均速度是多少?
小芸同学解法如下:
解:设李磊去时的平均速度是x千米/时,则返回时的平均速度是(1-![]() )x千米/时,由题意得:
)x千米/时,由题意得:![]() +
+![]() =7,…
=7,…
你认为小芸同学的解法正确吗?若正确,请写出该方程所依据的等量关系,并完成剩下的步骤;若不正确,请说明原因,并完整地求解问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
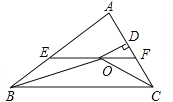
①EF=BE+CF;
②∠BOC=90°+![]() ∠A;
∠A;
③点O到△ABC各边的距离相等;
④设OD=m,AE+AF=n,则![]() .
.
其中正确的结论是____.(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com