
【题目】如图,直线y=﹣ ![]() x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A,B两点.
x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A,B两点.
(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的一点,连接PA、PB、PO,若△POA的面积是△POB面积的 ![]() 倍.
倍.
①求点P的坐标;
②点Q为抛物线对称轴上一点,请直接写出QP+QA的最小值;
(3)点M为直线AB上的动点,点N为抛物线上的动点,当以点O、B、M、N为顶点的四边形是平行四边形时,请直接写出点M的坐标.
【答案】
(1)解:∵直线y=﹣ ![]() x+1与x轴交于点A,与y轴交于点B,
x+1与x轴交于点A,与y轴交于点B,
∴A(2,0),B(0,1),
∵抛物线y=﹣x2+bx+c经过A、B两点,
∴ ![]() ,
,
∴ ![]()
∴抛物线解析式为y=﹣x2+ ![]() x+1
x+1
(2)解:①由(1)知,A(2,0),B(0,1),
∴OA=2,OB=1,
由(1)知,抛物线解析式为y=﹣x2+ ![]() x+1,
x+1,
∵点P是第一象限抛物线上的一点,
∴设P(a,﹣a2+ ![]() a+1),((a>0,﹣a2+
a+1),((a>0,﹣a2+ ![]() a+1>0),
a+1>0),
∴S△POA= ![]() OA×Py=
OA×Py= ![]() ×2×(﹣a2+
×2×(﹣a2+ ![]() a+1)=﹣a2+
a+1)=﹣a2+ ![]() a+1
a+1
S△POB= ![]() OB×Px=
OB×Px= ![]() ×1×a=
×1×a= ![]() a
a
∵△POA的面积是△POB面积的 ![]() 倍.
倍.
∴﹣a2+ ![]() a+1=
a+1= ![]() ×
× ![]() a,
a,
∴a= ![]() 或a=﹣
或a=﹣ ![]() (舍)
(舍)
∴P( ![]() ,1);
,1);
②如图1,
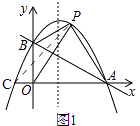
由(1)知,抛物线解析式为y=﹣x2+ ![]() x+1,
x+1,
∴抛物线的对称轴为x= ![]() ,抛物线与x轴的另一交点为C(﹣
,抛物线与x轴的另一交点为C(﹣ ![]() ,0),
,0),
∵点A与点C关于对称轴对称,
∴QP+QA的最小值就是PC= ![]()
(3)解:①当OB为平行四边形的边时,MN=OB=1,MN∥OB,
∵点N在直线AB上,
∴设M(m,﹣ ![]() m+1),
m+1),
∴N(m,﹣m2+ ![]() m+1),
m+1),
∴MN=|﹣m2+ ![]() m+1﹣(﹣
m+1﹣(﹣ ![]() m+1)|=|m2﹣2m|=1,
m+1)|=|m2﹣2m|=1,
Ⅰ、m2﹣2m=1,
解得,m=1± ![]() ,
,
∴M(1+ ![]() ,
, ![]() (1﹣
(1﹣ ![]() ))或M(1﹣
))或M(1﹣ ![]() ,
, ![]() (1+
(1+ ![]() ))
))
Ⅱ、m2﹣2m=﹣1,
解得,m=1,
∴M(1, ![]() );
);
②当OB为对角线时,OB与MN互相平分,交点为H,
∴OH=BH,MH=NH,
∵B(0,1),O(0,0),
∴H(0, ![]() ),
),
设M(n,﹣ ![]() n+1),N(d,﹣d2+
n+1),N(d,﹣d2+ ![]() d+1)
d+1)
∴ 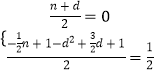 ,
,
∴ ![]() 或
或 ![]() ,
,
∴M(﹣(1+ ![]() ),
), ![]() (3+
(3+ ![]() ))或M(﹣(1﹣
))或M(﹣(1﹣ ![]() ),
), ![]() (3﹣
(3﹣ ![]() ));
));
即:满足条件的点M的坐标(1+ ![]() ,
, ![]() (1﹣
(1﹣ ![]() ))或(1﹣
))或(1﹣ ![]() ,﹣
,﹣ ![]() (1+
(1+ ![]() ))或(1,
))或(1, ![]() )或M(﹣(1+
)或M(﹣(1+ ![]() ),
), ![]() (3+
(3+ ![]() ))或M(﹣(1﹣
))或M(﹣(1﹣ ![]() ),
), ![]() (3﹣
(3﹣ ![]() ))
))
【解析】(1) 先通过直线解析式求AB求出坐标,再代入抛物线解析式 ;(2)设出P的坐标,用P的横坐标a表示其 纵坐标,再表示△POA的面积与△POB面积,按照题意列出关于a的方程;(3)利用对称法求两线段和最小值,A的对称点就是抛物线与x轴的另一个交点C,连接PC与对称轴相交即可求出Q点;(4)“以点O、B、M、N为顶点的四边形是平行四边形”可找出一对固定点,对它进行分类讨论: OB为平行四边形的边;OB为对角线,OB与MN互相平分;按照几何关系构建关于M的横坐标为未知数的方程求解.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,将一个边长为![]() 的正方形图形分割成四部分,观察图形,解答下列问题:
的正方形图形分割成四部分,观察图形,解答下列问题:
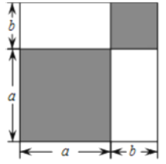
(1)根据图中条件,请用两种方法表示该阴影图形的总面积
方法1:_________________方法2__________________;
由此可得等量关系:______________________________;
应用该等量关系解决下列问题:
(2)若图中的a,b(![]() )满足
)满足![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抗击新冠病毒,保护学生和教师的生命安全,新希望中学![]() 元购进甲、乙两种医用口罩共计
元购进甲、乙两种医用口罩共计![]() 盒,甲,乙两种口罩的售价分别是
盒,甲,乙两种口罩的售价分别是![]() 元/盒,
元/盒,![]() 元/盒;甲,乙两 种口罩的数量分别是
元/盒;甲,乙两 种口罩的数量分别是![]() 个/盒,
个/盒,![]() 个/盒.
个/盒.
(1)求新希望中学甲、乙两种口罩各购进了多少盒?
(2)按照教育局要求,学校必须储备两周的用量,新希望中学师生共计![]() 人,每人每天
人,每人每天![]() 个口罩,问购买的口罩数量是否能满足教育局的要求?
个口罩,问购买的口罩数量是否能满足教育局的要求?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延长CA到O,使AO=AC,以O为圆心,OA长为半径作⊙O交BA延长线于点D,连接CD.
(1)求证:CD是⊙O的切线;
(2)若AB=4,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线OC、BC的函数关系式分别是y1=x和y2=﹣2x+6,直线BC与x轴交于点B,直线BA与直线OC相交于点A.
(1)当x取何值时y1>y2?
(2)当直线BA平分△BOC的面积时,求点A的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P在线段AB外,且PA=PB,求证:点P在线段AB的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )

A. 作∠APB的平分线PC交AB于点C
B. 过点P作PC⊥AB于点C且AC=BC
C. 取AB中点C,连接PC
D. 过点P作PC⊥AB,垂足为C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距72千米,李磊骑自行车往返两地一共用了7小时,已知他去时的平均速度比返回时的平均速度快![]() ,求李磊去时的平均速度是多少?
,求李磊去时的平均速度是多少?
小芸同学解法如下:
解:设李磊去时的平均速度是x千米/时,则返回时的平均速度是(1-![]() )x千米/时,由题意得:
)x千米/时,由题意得:![]() +
+![]() =7,…
=7,…
你认为小芸同学的解法正确吗?若正确,请写出该方程所依据的等量关系,并完成剩下的步骤;若不正确,请说明原因,并完整地求解问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标xOy中,正比例函数y=kx的图象与反比例函数y= ![]() 的图象都经过点A(2,﹣2).
的图象都经过点A(2,﹣2).
(1)分别求这两个函数的表达式;
(2)将直线OA向上平移3个单位长度后与y轴交于点B,与反比例函数图象在第四象限内的交点为C,连接AB,AC,求点C的坐标及△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形![]() 中,
中,![]() 为平面直角坐标系的原点,点
为平面直角坐标系的原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() 且
且![]() 满足
满足![]() ,点
,点![]() 在第一象限内,点
在第一象限内,点![]() 从原点出发,以每秒
从原点出发,以每秒![]() 个单位长度的速度沿着
个单位长度的速度沿着![]() 的线路移动.
的线路移动.
![]() 求点
求点![]() 的坐标为 ;当点
的坐标为 ;当点![]() 移动
移动![]() 秒时,点
秒时,点![]() 的坐标为
的坐标为
![]() 在移动过程中,当点
在移动过程中,当点![]() 移动
移动![]() 秒时,求
秒时,求![]() 的面积.
的面积.
![]() 在
在![]() 的条件下,坐标轴上是否存在点
的条件下,坐标轴上是否存在点![]() ,使
,使![]() 的面积与
的面积与![]() 的面积相等,若存在,求点
的面积相等,若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com