
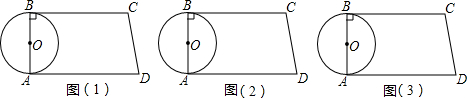
| 4 |
| 3 |
| 4 |
| 3 |
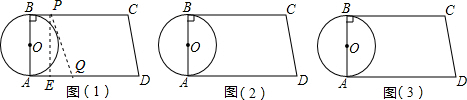 解:(1)由题意知:当t=16-3t,即t=4(秒)时,四边形PQDC是直角梯形;
解:(1)由题意知:当t=16-3t,即t=4(秒)时,四边形PQDC是直角梯形;| 4 |
| 3 |
| 4 |
| 3 |
| 16 |
| 3 |
| 4 |
| 3 |


科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:
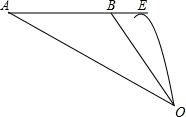 60°.飞机继续飞行0.1千米到达E处进行空投,已知空投物资在空中下落过程中的轨迹是抛物线,若要使空投物资刚好落在O处.
60°.飞机继续飞行0.1千米到达E处进行空投,已知空投物资在空中下落过程中的轨迹是抛物线,若要使空投物资刚好落在O处.查看答案和解析>>
科目:初中数学 来源: 题型:
| A | B | |
| 成本价(元/套) | 250 | 280 |
| 售价(元/套) | 300 | 340 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com