
【题目】某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.

(1)写出商场销售这种工具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
【答案】(1)w=-10x2+700x-10000;
(2)销售单价为35元时,每天销售利润最大,最大利润为2250元;
(3)方案A的最大利润更高,理由见解析.
【解析】试题分析:(1)根据利润=(销售单价-进价)×销售量,列出函数关系式即可;
(2)根据(1)式列出的函数关系式,运用配方法求最大值;
(3)分别求出方案A、B中x的取值范围,然后分别求出A、B方案的最大利润,然后进行比较.
试题解析:(1)w=(x-20)(250-10x+250)=-10x2+700x-10000.
(2)w=-10x2+700x-10000=-10(x-35)2+2250.
所以,当x=35时,w有最大值2250.
即销售单价为35元时,该文具每天的销售利润最大.
(3)方案A:由题可得20<x≤30,
因为a=-10<0,对称轴为x=35,
抛物线开口向下,在对称轴左侧,w随x的增大而增大,
所以,当x=30时,w取最大值为2000元.
方案B:由题意得![]() ,解得:
,解得: ![]() ,
,
在对称轴右侧,w随x的增大而减小,
所以,当x=45时,w取最大值为1250元.
因为2000元>1250元,
所以选择方案A.


科目:初中数学 来源: 题型:
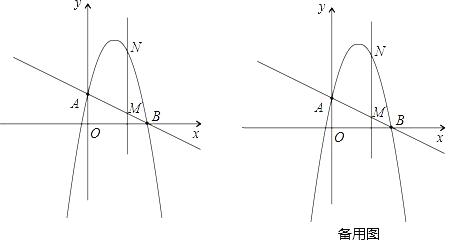
【题目】如图,一次函数![]() 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,A点表示2,现在点A向右移动两个单位后到达点B;再向左移动10个单位到达C点:
(1)请在数轴上表示出A点开始移动时位置及B、C点位置;
(2)当A点移动到C点时,若要再移动到原点,问必须向哪个方向移动多少个单位?
(3)请把A点从开始移动直至到达原点这一过程,用一个有理数算式表达出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某镇道路改造工程,由甲、乙两工程队合作完成.甲工程队单独施工比乙工程队单独施工多用30天完成此项工程,甲工程队30天完成的工程与甲、乙两工程队10天完成的工程相等.
(1)求甲、乙两工程队单独完成此项工程各需要多少天?
(2)如果甲工程队施工每天需付施工费1万元,乙工程队施工每天需付施工费2.5万元,甲工程队至少要单独施工多少天后,再由甲、乙两工程队合作施工完成剩下的工程,才能使施工费不超过64万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
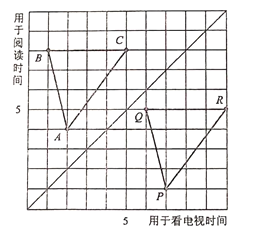
【题目】图中,点A,B,C,P,Q,R显示了6名学生平均每周用于阅读课外书的时间和用于看电视的时间(单位:h)
(1)用有序数对表示图中点A,B,C,P,Q,R
(2)图中方格纸的对角线的左上方的点有什么共同的特点?它右下方的点呢?
(3)三角形ABC的图形经过怎样的变换后得到三角形PQR的图形?其中点A对应点P,点B对应点Q,点C对应点R
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.

(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b≥(x-2)2+m的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
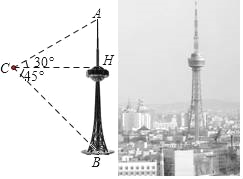
【题目】吉林省广播电视塔(简称“吉塔”)是我省目前最高的人工建筑,也是俯瞰长春市美景的最佳去处.某科技兴趣小组利用无人机搭载测量仪器测量“吉塔”的高度.已知如图将无人机置于距离“吉塔”水平距离138米的点C处,则从无人机上观测塔尖的仰角恰为30°,观测塔基座中心点的俯角恰为45°.求“吉塔”的高度.(注: ![]() ≈1.73,结果保留整数)
≈1.73,结果保留整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com