
【题目】如图1,E为矩形ABCD边AD上一点,点P从点C沿折线CD﹣DE﹣EB运动到点B时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是( )
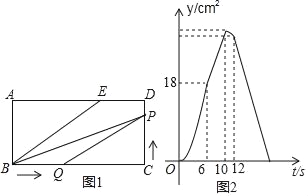
A.AE=8cm
B.sin∠EBC=![]()
C.当10≤t≤12时,![]()
D.当t=12s时,△PBQ是等腰三角形
【答案】D
【解析】
观察图象可知:点P在CD上运动的时间为6s,在DE上运动的时间为4s,点Q在BC上运动的时间为12s,所以CD=6,DE=4,BC=12,然后结合三角函数、三角形的面积等逐一进行判断即可得.
观察图象可知:点P在CD上运动的时间为6s,在DE上运动的时间为4s,点Q在BC上运动的时间为12s,
所以CD=6,DE=4,BC=12,
∵AD=BC,
∴AD=12,
∴AE=12﹣4=8cm,故A正确,
在Rt△ABE中,∵AE=8,AB=CD=6,
∴BE=![]() =10,
=10,
∴sin∠EBC=sin∠AEB=![]() ,故B正确,
,故B正确,
当10≤t≤12时,点P在BE上,BP=10﹣(t﹣10)=20﹣t,
∴S△BQP=![]() t(20﹣t)
t(20﹣t)![]() =﹣
=﹣![]() t2+6t,故C正确,
t2+6t,故C正确,
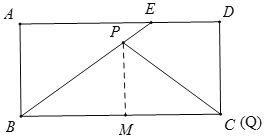
如图,当t=12时,Q点与C点重合,点P在BE上,此时BP=20-12=8,过点P作PM⊥BC于M,
在Rt△BPM中,cos∠PBM=![]() ,
,
又∠PBM=∠AEB,在Rt△ABE中,cos∠AEB=![]() ,
,
∴![]() ,
,
∴BM=6.4,∴QM=12-6.4=5.6,
∴BP≠PC,即△PBQ不是等腰三角形,故D错误,
故选D.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=Rt∠,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AD=16,DE=10,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )

A. 56° B. 62° C. 68° D. 78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,点![]() ,以线段
,以线段![]() 为直径作圆,圆心为
为直径作圆,圆心为![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:直线![]() 是
是![]() 的切线;
的切线;
(2)点![]() 为
为![]() 轴上任意一动点,连接
轴上任意一动点,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() :
:
①当![]() 时,求所有
时,求所有![]() 点的坐标 (直接写出);
点的坐标 (直接写出);
②求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】英语老师对某班级全班同学进行口语测试,并按10分制评分,将评分结果制成了如图两幅统计图(不完整).请根据图表信息,解答下列问题:
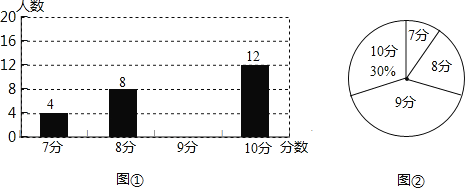
(1)求该班级学生总人数,并将条形统计图补充完整;
(2)求该班学生口语测试所得分数的平均分;
(3)英语老师将随机邀请该班一名同学进行口语对话,求事件“英语老师邀请得分为9分的同学进行口语对话”发生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
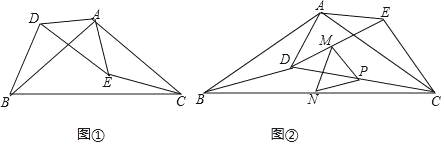
【题目】如图①,在等腰△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE=120°.
(1)求证:△ABD≌△ACE;
(2)把△ADE绕点A逆时针方向旋转到图②的位置,连接CD,点M、P、N分别为DE、DC、BC的中点,连接MN、PN、PM,判断△PMN的形状,并说明理由;
(3)在(2)中,把△ADE绕点A在平面内自由旋转,若AD=4,AB=6,请分别求出△PMN周长的最小值与最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
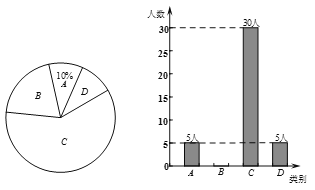
【题目】为了解阳光社区年龄20~60岁居民对垃圾分类的认识,学校课外实践小组随机抽取了该社区、该年龄段的部分居民进行了问卷调查,并将调查数据整理后绘成如下两幅不完整的统计图.图中A表示“全部能分类”,B表示“基本能分类”,C表示“略知一二”,D表示“完全不会”.请根据图中信息解答下列问题:
(1)补全条形统计图并填空:被调查的总人数是 人,扇形图中D部分所对应的圆心角的度数为 ;
(2)若该社区中年龄20~60岁的居民约3000人,请根据上述调查结果,估计该社区中C类有多少人?
(3)根据统计数据,结合生活实际,请你对社区垃圾分类工作提一条合理的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
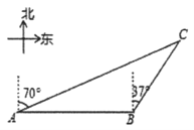
【题目】2019年12月17日,我国第一艘国产航母“山东舰”在海南三亚交付海军.在民族复兴的路上我们伟大的祖国又前进了一大步!如图,“山东舰”在一次试水测试中,由东向西航行到达![]() 处时,测得小岛
处时,测得小岛![]() 位于距离航母30海里的北偏东37°方向.“山东舰”再向西匀速航行1.5小时后到达
位于距离航母30海里的北偏东37°方向.“山东舰”再向西匀速航行1.5小时后到达![]() 处,此时测得小岛
处,此时测得小岛![]() 位于航母的北偏东70°方向.
位于航母的北偏东70°方向.
(1)![]() _______°;
_______°;
(2)求航母的速度.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com