
【题目】已知在平面直角坐标系中,点![]() ,以线段
,以线段![]() 为直径作圆,圆心为
为直径作圆,圆心为![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:直线![]() 是
是![]() 的切线;
的切线;
(2)点![]() 为
为![]() 轴上任意一动点,连接
轴上任意一动点,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() :
:
①当![]() 时,求所有
时,求所有![]() 点的坐标 (直接写出);
点的坐标 (直接写出);
②求![]() 的最大值.
的最大值.
科目:初中数学 来源: 题型:
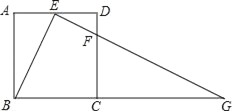
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF:DC=1:4,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为10,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线经过点O(0,0)与点A(4,0),顶点为点P,且最小值为-2.
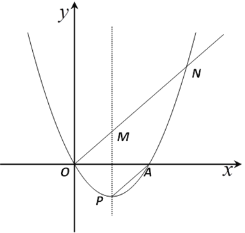
(1)求抛物线的表达式;
(2)过点O作PA的平行线交抛物线对称轴于点M,交抛物线于另一点N,求ON的长;
(3)抛物线上是否存在一个点E,过点E作x轴的垂线,垂足为点F,使得△EFO∽△AMN,若存在,试求出点E的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区域平面示意图如图,点O在河的一侧,AC和BC表示两条互相垂直的公路.甲勘测员在A处测得点O位于北偏东45°,乙勘测员在B处测得点O位于南偏西73.7°,测得AC=840m,BC=500m.请求出点O到BC的距离.参考数据:sin73.7°≈![]() ,cos73.7°≈
,cos73.7°≈![]() ,tan73.7°≈
,tan73.7°≈![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
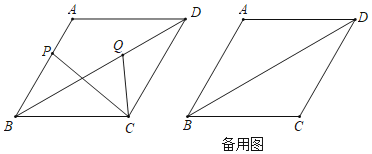
【题目】已知菱形ABCD中,AB=4,∠BAD=120°,点P是直线AB上任意一点,连接PC,在∠PCD内部作射线CQ与对角线BD交于点Q(与B、D不重合),且∠PCQ=30°.
(1)如图,当点P在边AB上,且BP=3时,求PC的长;
(2)当点P在射线BA上,且BP=n(0≤n<8)时,求QC的长;(用含n的式子表示)
(3)连接PQ,直线PQ与直线BC相交于点E,如果△QCE与△BCP相似,请直接写出线段BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,E为矩形ABCD边AD上一点,点P从点C沿折线CD﹣DE﹣EB运动到点B时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是( )
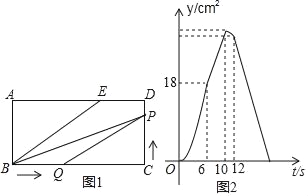
A.AE=8cm
B.sin∠EBC=![]()
C.当10≤t≤12时,![]()
D.当t=12s时,△PBQ是等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
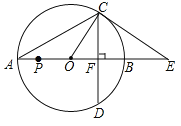
【题目】如图,以AB为直径的⊙O与CE相切于点C,CE交AB的延长线于点E,直径AB=18,∠A=30°,弦CD⊥AB,垂足为点F,连接AC,OC,则下列结论正确的是______.(写出所有正确结论的序号)
①![]() ;
;
②扇形OBC的面积为![]() π;
π;
③△OCF∽△OEC;
④若点P为线段OA上一动点,则APOP有最大值20.25.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,利用直尺和圆规,分别以
中,利用直尺和圆规,分别以![]() 、
、![]() 为圆心,相同的长度为半径(半径大于线段
为圆心,相同的长度为半径(半径大于线段![]() 的一半)作四段弧,分别交于
的一半)作四段弧,分别交于![]() 、
、![]() 两点,连接
两点,连接![]() 、
、![]() ,分别交
,分别交![]() 、
、![]() 于
于![]() 、
、![]() ,连接
,连接![]() 、
、![]() ,则四边形
,则四边形![]() 为( )
为( )
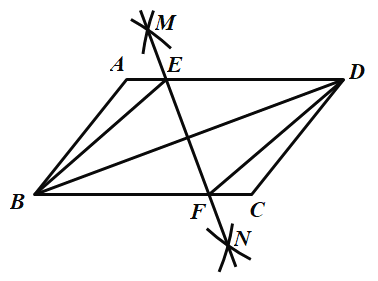
A.梯形B.平行四边形C.矩形D.菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com