
【题目】抛物线经过点O(0,0)与点A(4,0),顶点为点P,且最小值为-2.
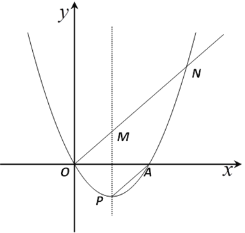
(1)求抛物线的表达式;
(2)过点O作PA的平行线交抛物线对称轴于点M,交抛物线于另一点N,求ON的长;
(3)抛物线上是否存在一个点E,过点E作x轴的垂线,垂足为点F,使得△EFO∽△AMN,若存在,试求出点E的坐标;若不存在请说明理由.
【答案】(1)抛物线的表达式为![]() ,(或
,(或![]() );(2)
);(2)![]() ;(3)抛物线上存在点E,使得△EFO∽△AMN,这样的点共有2个,分别是(
;(3)抛物线上存在点E,使得△EFO∽△AMN,这样的点共有2个,分别是(![]() ,
,![]() )和(
)和(![]() ,
,![]() ).
).
【解析】
(1)由点O(0,0)与点A(4,0)的纵坐标相等,可知点O、A是抛物线上的一对对称点,所以对称轴为直线x=2,又因为最小值是-2,所以顶点为(2,-2),利用顶点式即可用待定系数法求解;
(2)设抛物线对称轴交![]() 轴于点D、N(
轴于点D、N(![]() ,
,![]() ),先求出
),先求出![]() =45°,由ON∥PA,依据平行线的性质得到
=45°,由ON∥PA,依据平行线的性质得到![]() =45°,依据等腰直角三角形两直角边的关系可得到
=45°,依据等腰直角三角形两直角边的关系可得到![]() =
=![]() ,解出即可得到点N的坐标,再运用勾股定理求出ON的长度;
,解出即可得到点N的坐标,再运用勾股定理求出ON的长度;
(3)先运用勾股定理求出AM和OM,再用ON-OM得MN,运用相似三角形的性质得到EF:FO的值,设E(![]() ,
,![]() ),分点E在第一象限、第二或四象限讨论,依据EF:FO=1
),分点E在第一象限、第二或四象限讨论,依据EF:FO=1
:2列出关于m的方程解出即可.
解:(1)∵抛物线经过点O(0,0)与点A(4,0),
∴对称轴为直线x=2,
又∵顶点为点P,且最小值为-2,,
∴顶点P(2,-2),
∴设抛物线的表达式为![]()
将O(0,0)坐标代入,解得![]()
∴抛物线的表达式为![]() ,即
,即![]() ;
;
(2)设抛物线对称轴交![]() 轴于点D,
轴于点D,
∵顶点P坐标为(2,-2),
∴点D坐标为(2,0)
又∵A(4,0),
∴△ADP是以![]() 为直角的等腰直角三角形,
为直角的等腰直角三角形,![]() =45°
=45°
又∵ON∥PA ,
∴![]() =45°
=45°
∴若设点N的坐标为(![]() ,
,![]() )则
)则![]() =
=![]()
解得![]() ,
,
∴点N的坐标为(![]() ,
,![]() )
)
∴![]()
(3)抛物线上存在一个点E,使得△EFO∽△AMN,理由如下:
连接PO、AM,
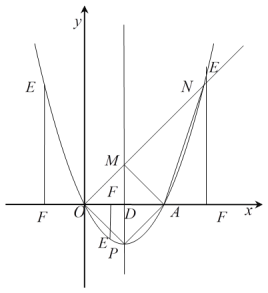
∵![]() =45°,
=45°,![]() =90°,
=90°,
∴![]() ,
,
又∵由点D坐标为(2,0),得OD=2,
∴![]() ,
,
又∵![]() =90°,由A(4,0),D(2,0)得AD=2,
=90°,由A(4,0),D(2,0)得AD=2,
∴![]() ,
,
同理可得![]() ,
,
∴![]() ,
,
∴AM:MN=![]() :
:![]() =1:2
=1:2
∵△EFO∽△AMN
∴EF:FO=AM:MN=1:2
设点E的坐标为(![]() ,
,![]() )(其中
)(其中![]() ),
),
①当点E在第一象限时,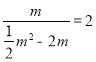 ,
,
解得![]() ,此时点E的坐标为(
,此时点E的坐标为(![]() ,
,![]() ),
),
②当点E在第二象限或第四象限时,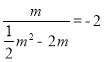 ,
,
解得![]() ,此时点E的坐标为(
,此时点E的坐标为(![]() ,
,![]() )
)
综上所述,抛物线上存在一个点E,使得△EFO∽△AMN,这样的点共有2个,分别是(![]() ,
,![]() )和(
)和(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
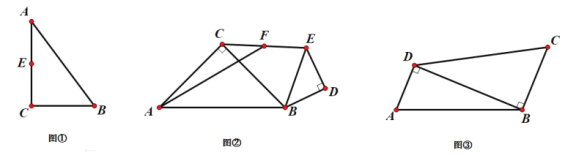
【题目】问题发现:
(1)如图①,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 边上,将
边上,将![]() 沿着
沿着![]() 折叠后得到
折叠后得到![]() ,连接
,连接![]() 并使得
并使得![]() 最小,请画出符合题意的点
最小,请画出符合题意的点![]() ;
;
问题探究:
(2)如图②,已知在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,求
,求![]() 的最大值;
的最大值;
问题解决:
(3)西安大明宫遗址公园是世界文化遗产,全国重点文物保护单位,为了丰富同学们的课外学习生活,培养同学们的探究实践能力,周末光明中学的张老师在家委会的协助下,带领全班同学去大明宫开展研学活动.在公园开设的一处沙地考古模拟场地上,同学们参加了一次模拟考古游戏.张老师为同学们现场设计了一个四边形![]() 的活动区域,如图③所示,其中
的活动区域,如图③所示,其中![]() 为一条工作人员通道,同学们的入口设在点
为一条工作人员通道,同学们的入口设在点![]() 处,
处,![]() ,
,![]() ,
,![]() ,
,![]() 米.在上述条件下,小明想把宝物藏在距入口
米.在上述条件下,小明想把宝物藏在距入口![]() 尽可能远的
尽可能远的![]() 处让小鹏去找,请问小明的想法是否可以实现?如果可以,请求出
处让小鹏去找,请问小明的想法是否可以实现?如果可以,请求出![]() 的最大值及此时
的最大值及此时![]() 区域的面积,如果不能,请说明理由.
区域的面积,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=Rt∠,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AD=16,DE=10,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
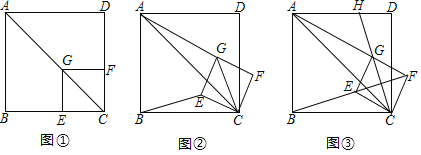
【题目】如图![]() ,已知点G在正方形ABCD的对角线AC上,
,已知点G在正方形ABCD的对角线AC上,![]() ,垂足为点E,
,垂足为点E,![]() ,垂足为点F.
,垂足为点F.
![]() 发现问题:在图
发现问题:在图![]() 中,
中,![]() 的值为______.
的值为______.
![]() 探究问题:将正方形CEGF绕点C顺时针方向旋转
探究问题:将正方形CEGF绕点C顺时针方向旋转![]() 角
角![]() ,如图
,如图![]() 所示,探究线段AG与BE之间的数量关系,并证明你的结论.
所示,探究线段AG与BE之间的数量关系,并证明你的结论.
![]() 解决问题:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图
解决问题:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图![]() 所示,延长CG交AD于点H;若
所示,延长CG交AD于点H;若![]() ,
,![]() ,直接写出BC的长度.
,直接写出BC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为争创文明城市,我市交警部门在全市范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车戴安全帽情况进行问卷调查,并将两次收集的数据制成如下统计图表.

类别 | 人数 | 百分比 |
A | 68 | 6.8% |
B | 245 | b% |
C | a | 51% |
D | 177 | 17.7% |
总计 | c | 100% |
根据以上提供的信息解决下列问题:
(1)a= ,b= c=
(2)若我市约有30万人使用电瓶车,请分别计算活动前和活动后全市骑电瓶车“都不戴”安全帽的人数.
(3)经过某十字路口,汽车无法继续直行只可左转或右转,电动车不受限制,现有一辆汽车和一辆电动车同时到达该路口,用画树状图或列表的方法求汽车和电动车都向左转的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以40m/s的速度将小球沿与地面30°角的方向击出时,小球的飞行路线是一段抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系式为h=20t-![]()
![]() (t≥0). 回答问题:
(t≥0). 回答问题:

(1)小球的飞行高度能否达到19.5m;
(2) 小球从最高点到落地需要多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )

A. 56° B. 62° C. 68° D. 78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,点![]() ,以线段
,以线段![]() 为直径作圆,圆心为
为直径作圆,圆心为![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:直线![]() 是
是![]() 的切线;
的切线;
(2)点![]() 为
为![]() 轴上任意一动点,连接
轴上任意一动点,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() :
:
①当![]() 时,求所有
时,求所有![]() 点的坐标 (直接写出);
点的坐标 (直接写出);
②求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年12月17日,我国第一艘国产航母“山东舰”在海南三亚交付海军.在民族复兴的路上我们伟大的祖国又前进了一大步!如图,“山东舰”在一次试水测试中,由东向西航行到达![]() 处时,测得小岛
处时,测得小岛![]() 位于距离航母30海里的北偏东37°方向.“山东舰”再向西匀速航行1.5小时后到达
位于距离航母30海里的北偏东37°方向.“山东舰”再向西匀速航行1.5小时后到达![]() 处,此时测得小岛
处,此时测得小岛![]() 位于航母的北偏东70°方向.
位于航母的北偏东70°方向.
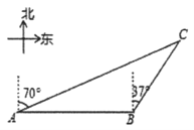
(1)![]() _______°;
_______°;
(2)求航母的速度.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com