
【题目】问题发现:
(1)如图①,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 边上,将
边上,将![]() 沿着
沿着![]() 折叠后得到
折叠后得到![]() ,连接
,连接![]() 并使得
并使得![]() 最小,请画出符合题意的点
最小,请画出符合题意的点![]() ;
;
问题探究:
(2)如图②,已知在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,求
,求![]() 的最大值;
的最大值;
问题解决:
(3)西安大明宫遗址公园是世界文化遗产,全国重点文物保护单位,为了丰富同学们的课外学习生活,培养同学们的探究实践能力,周末光明中学的张老师在家委会的协助下,带领全班同学去大明宫开展研学活动.在公园开设的一处沙地考古模拟场地上,同学们参加了一次模拟考古游戏.张老师为同学们现场设计了一个四边形![]() 的活动区域,如图③所示,其中
的活动区域,如图③所示,其中![]() 为一条工作人员通道,同学们的入口设在点
为一条工作人员通道,同学们的入口设在点![]() 处,
处,![]() ,
,![]() ,
,![]() ,
,![]() 米.在上述条件下,小明想把宝物藏在距入口
米.在上述条件下,小明想把宝物藏在距入口![]() 尽可能远的
尽可能远的![]() 处让小鹏去找,请问小明的想法是否可以实现?如果可以,请求出
处让小鹏去找,请问小明的想法是否可以实现?如果可以,请求出![]() 的最大值及此时
的最大值及此时![]() 区域的面积,如果不能,请说明理由.
区域的面积,如果不能,请说明理由.
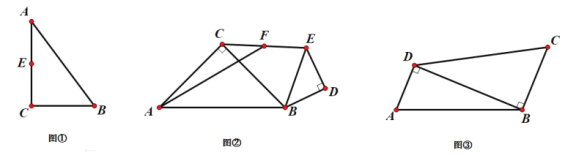
【答案】(1)作图见详解;
(2)![]() 的最大值是:
的最大值是:![]() ;
;
(3)![]() 的最大值为
的最大值为![]() ,此时
,此时![]() 区域的面积为
区域的面积为![]() .
.
【解析】
(1)根据题意判断出点![]() 的运动轨迹即可得解;
的运动轨迹即可得解;
(2)如图②中,取![]() 的中点
的中点![]() ,连接
,连接![]() 即可求解;
即可求解;
(3)如图③中,作![]() 的外接圆
的外接圆![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,证明
,证明![]() 是等边三角形,
是等边三角形,![]() ,由
,由![]() 可以推出点
可以推出点![]() 的运动轨迹是圆弧,不妨设圆心为
的运动轨迹是圆弧,不妨设圆心为![]() ,连接
,连接![]() 则
则![]() 求出
求出![]() ,即可求解.
,即可求解.
(1)![]()
![]() 是由
是由![]() 沿着
沿着![]() 折叠后得到
折叠后得到
![]()
![]()
![]() 点
点![]() 的运动轨迹是以点
的运动轨迹是以点![]() 为圆心,以
为圆心,以![]() 为半径的圆
为半径的圆
![]() 要使
要使![]() 最小,只能是当
最小,只能是当![]() 三点共线时
三点共线时
作图如下所示:
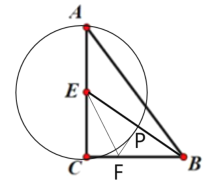
(2)如图②中,取![]() 的中点
的中点![]() ,连接
,连接![]()
∵![]()
∴![]()
∴![]()
∴![]() ,
,
∵![]()
∴![]()
∵![]() ,
,
∴![]()
∴![]() 的最大值是
的最大值是![]() ;
;
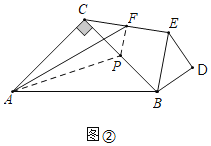
(3)如图③中,作![]() 的外接圆
的外接圆![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
∵![]()
∴![]()
∴![]()
∵![]()
∴![]() 是等边三角形,
是等边三角形,![]()
∵![]()
∴点![]() 的运动轨迹是圆弧,不妨设圆心为
的运动轨迹是圆弧,不妨设圆心为![]() ,连接
,连接![]() 则
则![]()
作![]() 于
于![]() ,在
,在![]() 中,
中,![]()
∴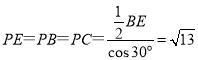
∵![]()
∴![]()
在![]() 中,
中,![]()
∵![]() ,
,
∴![]()
∴![]() 的最大值为
的最大值为![]() ,此时
,此时![]() 共线,如图③﹣1中,作
共线,如图③﹣1中,作![]() 于
于![]()
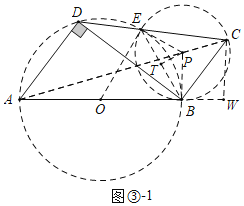
∵![]()
∴![]()
![]()
![]()
∴![]()
![]()
![]()
∴![]()


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,将点
,将点![]() 向右平移6个单位长度,得到点
向右平移6个单位长度,得到点![]() .
.
(1)直接写出点![]() 的坐标;
的坐标;
(2)若抛物线![]() 经过点
经过点![]() ,求
,求![]() 的值;
的值;
(3)若抛物线![]() 与线段
与线段![]() 有且只有一个公共点时,求抛物线顶点横坐标
有且只有一个公共点时,求抛物线顶点横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,将抛物线y=﹣x2+bx+c与直线y=﹣x+1相交于点A(0,1)和点B(3,﹣2),交x轴于点C,顶点为点F,点D是该抛物线上一点.
(1)求抛物线的函数表达式;
(2)如图1,若点D在直线AB上方的抛物线上,求△DAB的面积最大时点D的坐标;
(3)如图2,若点D在对称轴左侧的抛物线上,且点E(1,t)是射线CF上一点,当以C、B、D为顶点的三角形与△CAE相似时,求所有满足条件的t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() 且经过点
且经过点![]() 动直线
动直线![]() 的解析式为
的解析式为![]()
![]() .
.
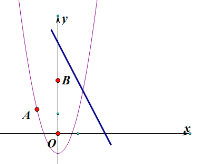
(1)求抛物线![]() 的解析式;
的解析式;
(2)将抛物线![]() 向上平移一个单位得到新的抛物线
向上平移一个单位得到新的抛物线![]() ,过点
,过点![]() 的直线交抛物线于
的直线交抛物线于![]() 两点(
两点(![]() 点位于
点位于![]() 点的左边),动直线
点的左边),动直线![]() 过点
过点![]() ,与抛物线
,与抛物线![]() 的另外一个交点为点
的另外一个交点为点![]() 求证:直线
求证:直线![]() 恒过一个定点;
恒过一个定点;
(3)已知点![]() ,且点
,且点![]() 在动直线
在动直线![]() 上,若
上,若![]() 是以
是以![]() 为顶角的等腰三角形,这样的等腰三角形有且只存在一个,请求出
为顶角的等腰三角形,这样的等腰三角形有且只存在一个,请求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
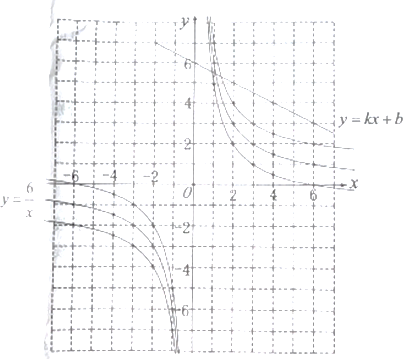
【题目】图象是函数性质的直观载体,通过图象我们容易把握函数的整体性质.下面我们就一类特殊的函数展开探究.经历分析解析式、列表、描点、连线过程得到函数![]() 、
、![]() 、
、![]() 的图象如下图所示.
的图象如下图所示.
(1)观察发现:三个函数的图象都是双曲线,且分别关于直线![]() 、
、![]() 、
、![]() 对称:三个函数解析式中分式部分完全相同,则图象的大小和形状完全相同,只有位置和对称轴发生了变化.因此,我们可以通过描点或平移的方法画函数图象.平移函数
对称:三个函数解析式中分式部分完全相同,则图象的大小和形状完全相同,只有位置和对称轴发生了变化.因此,我们可以通过描点或平移的方法画函数图象.平移函数![]() 的图象可以得到函数
的图象可以得到函数![]() 、
、![]() 的图象,分别写出平移的方向和距离.
的图象,分别写出平移的方向和距离.
(2)探索思考:在所给的平面直角坐标系中,请用你喜欢的方法画出函数![]() 图象,并写出这个函数的一条性质.
图象,并写出这个函数的一条性质.
(3)拓展应用:若直线![]() 过点
过点![]() 、
、![]() ,结合你所画的函数图象,直接写出不等式
,结合你所画的函数图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
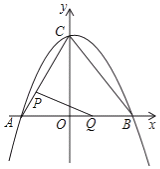
【题目】如图,在平面直角坐标系中,二次函数y=﹣![]() x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
(1)求二次函数的解析式;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)点M在抛物线上,且△AOM的面积与△AOC的面积相等,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
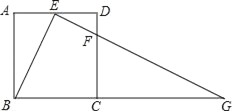
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF:DC=1:4,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为10,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线经过点O(0,0)与点A(4,0),顶点为点P,且最小值为-2.
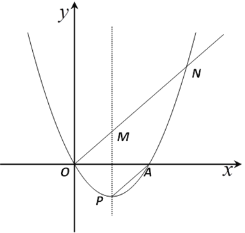
(1)求抛物线的表达式;
(2)过点O作PA的平行线交抛物线对称轴于点M,交抛物线于另一点N,求ON的长;
(3)抛物线上是否存在一个点E,过点E作x轴的垂线,垂足为点F,使得△EFO∽△AMN,若存在,试求出点E的坐标;若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com